함수의 극한

수열의 극한은 양의 정수의 집합 위에서 정의된 실함수의 극한이라 할 수 있다. 극한의 개념은 실수의 임의의 구간 위의 모든 점에서 정의된 함수에서 특히 중요하다.

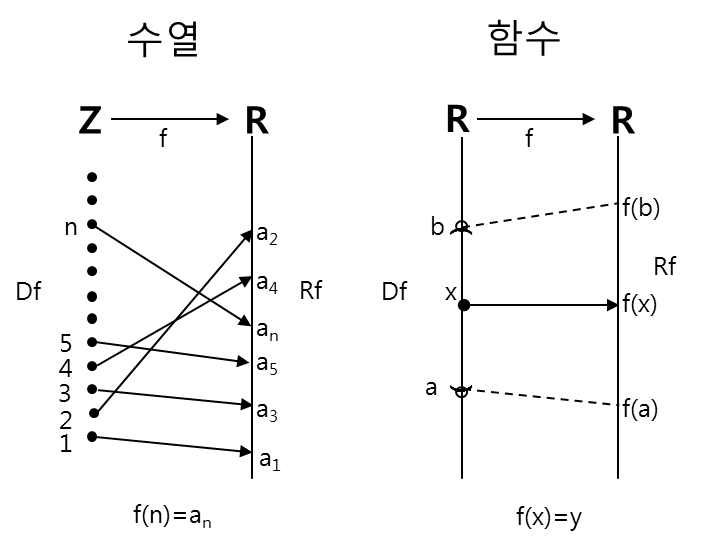
수열 \(\{a_n\}\)의 극한에서는 n이 한없이 커질 때 \(a_n\)이 어떤 값에 근접하는 가를 조사하였다. 연속변수 함수 f(x)의 극한에서는 x가 어떤 값 a에 가까와질 때 f(x)가 어떤 값에 근접하는 가를 조사한다.

[예제 1] 다음 2개의 함수에서 x가 1에 가까와질 때 f(x)는 어떤 값에 가까와지는가를 조사하여라.

\[(1)\ f(x)=x+1\qquad(2)\ f(x)=\frac{x^2-1}{x-1}\]

<풀이> 아래 그래프에서 x가 1에 가까와질 때 함수 값은 모두 2에 한없이 가까와 진다.

 

정의 1 (함수의 극한) 함수 f는 a를 포함하는 구간 내의 모든 점에서 정의되어 있다(a에서는 정의되어 있지 않아도 된다). x가 a에 한없이 가까와질 때 가까와지는 방법에 무관하게 f(x)가 일정한 실수 α에 한없이 가까와지면 α를 x가 a에 가까와질 때의 f(x)의 극한 또는 극한값이라 하고, 기호로는

\[\lim_{x\to a}f(x)=\alpha\qquad\text{또는}\qquad x\to a\ \text{일 때}\ f(x)\to\alpha\]

로 나타낸다.

\(\lim_{x\to a}f(x)=\alpha\) 일 때 다음 두 조건을 만족하는 수열 \(\{x_n\}\)을 생각한다.
(1) \(x_n\in D_f,\,x_n\ne a,\,n=1,\,2,\,3,\,\cdots\)
(2) \(\lim_{x\to\infty}x_n=a\)

이 때 수열 \(x_1,\,x_2,\,\cdots,\,x_n,\,\cdots\)에 대하여 함수 f값의 수열 \(f(x_1),\,f(x_2),\,\cdots,\,f(x_n),\,\cdots\)이 정해진다. 가정에 의하여 x→a 일 때 f(x)→α 이므로 정의 1과 (2)에 의하여 \(f(x_n)\)→α 이다.

그런데 x→a 일 때 위의 두 조건을 만족하는 수열 \(\{a_n\}\)이 항상 존재한다. 수열의 극한의 정의에 따라서 임의의 ε>0에 대하여 자연수 N이 정해져서 n≥N 이면 \(|f(x_n)-\alpha|<\epsilon\) 이다. f의 값이 이 부등식을 만족하는 수열은 \(x_N,\,x_{N+1},\,x_{N+2},\,\cdots\) 이다. 이 수열은 원수열 \(\{a_n\}\)에서 처음 (N-1)개의 항을 제외한 것이므로 a에 수렴하고, a의 부근에 밀집되어 있다. 즉, 모든 항이 a의 어떤 근방에 속한다. 이 근방은 양수 δ를 선택하여 |a-x|<δ로 나타내어진다.

정의 2 (ε-δ에 의한 함수의 극한) 함수 f는 a를 포함하는 구간내의 모든 점에서 정의되어 있다(x=a에서는 정의되지 않아도 좋다). 임의의 ε>0에 대하여 양수 δ가 정해지고 0<|a-x|<δ를 만족하는 모든 x에 대하여 |f(x)-α|<ε 이면 x→a 일 때 f(x)→α 또는

\[\lim_{x\to a}f(x)=\alpha\]

로 나타내고, α를 x가 a에 가까와질 때의 극한 또는 극한값이라 한다.

[예제 2] f(x)=x+1 일 때 \(\lim_{x\to1}f(x)=2\) 임을 증명하여라.

<증명> |f(x)-2|=|(x+1)-2|=|x-1| 이므로 δ=ε(>0)이라 하면 0<|x-1|<δ인 모든 x에 대하여 |f(x)-2|<ε 이다. \(\therefore\ \lim_{x\to1}f(x)=2\).

[예제 3] f(x)=x 일 때 임의의 실수 a에 대하여 \(\lim_{x\to a}f(x)=a\) 임을 보여라.

<증명> |f(x)-a|=|x-a| 이므로 δ=ε(>0)이라 하면 0<|x-a|<δ인 모든 x에 대하여 |f(x)-a|<ε 이다. \(\therefore\ \lim_{x\to a}f(x)=a\).

[예제 4] f(x)=k(상수) 일 때 임의의 실수 a에 대하여 \(\lim_{x\to a}f(x)=k\) 임을 보여라.

<증명> 임의의 ε>0에 대하여 |f(x)-k|=|k-k|=0<ε. 이는 x에 무관하게 성립하므로 임의로 δ>0를 정하여도 0<|x-a|<δ인 모든 x에 대하여 |f(x)-k|<ε 이다. \(\therefore\ \lim_{x\to a}f(x)=k\).

[예제 5] \(f(x)=\frac{3x^2-12}{x-2}\)라 할 때 \(\lim_{x\to2}f(x)\)를 구하여라.

<풀이> x≠2 이면 \(f(x)=\frac{3(x-2)(x+2)}{x-2}=3(x+2)\). 따라서 x→2 일 때 f(x)→12로 추정된다. ε>0가 주어지고 x≠2 일 때 |f(x)-12|=|3(x+2)-12|=3|x-2|<ε 이다. 곧, |x-2|<ε/3. 따라서 δ=ε/3 이면 0<|x-2|<δ인 모든 x에 대하여 |f(x)-12|<ε 이다. \(\therefore\ \lim_{x\to2}f(x)=12\).

함수 f에 대하여 x→a 일 때 f(x)→α라 하자. 여기서 x→a 곧, x가 a에 가까와 질 때는 「x가 가까와지는 방법에 관계없이 a에 가까와질 때」라는 뜻을 포함한다.

(a) 실수전체에서 다음과 같이 정의된 Dirichlet의 함수 f를 생각해 보자.

\[f(x)=\begin{cases}1:\text{x가 유리수일 때}\\0:\text{x가 무리수일 때}\end{cases}\]

수열 \(a_1,\,a_2,\,a_3,\,\cdots,\,a_n,\,\cdots\)의 각 항이 모두 유리수이고, n→∞ 일 때 \(a_n\)→0 이라고 하면 수열 \(f(a_1),\,f(a_2),\,f(a_3)\,\cdots,\,f(a_n),\,\cdots\)의 각 항은 모두 1 이므로

\[\lim_{n\to\infty}f(a_n)=1\]

또한 수열 \(b_1,\,b_2,\,b_3,\,\cdots,\,b_n,\,\cdots\)의 각 항은 무리수이고, n→∞ 일 때 \(b_n\)→0 이라고 하면 수열 \(f(b_1),\,f(b_2),\,f(b_3),\,\cdots,\,f(b_n),\,\cdots\)의 각 항은 0 이므로

\[\lim_{n\to\infty}f(b_n)=0\]

곧, x가 0에 가까와질 때 그 방법에 따라 f(x)의 값은 다른값에 수렴한다. 따라서 x→0 일 때 f(x)의 극한값은 존재하지 않는다. 임의의 실수 \(x_0\)에 대하여도 같은 방법으로 f(x)의 극한값은 존재하지 않는다.

(b) f(x)=[x] (함수와 그래프 문제 1.(1) 참조)라 하자.

만약 x가 양의 값을 가지면서 0에 가까와지면 f(x)는 0에 한없이 가까와진다. 그러나 x가 음의 값을 가지면서 0에 가까와지면 f(x)는 -1에 한없이 가까와진다. 이 경우도 x가 0에 가까와지는 방법에 따라 다른 값에 수렴한다. 따라서 x→0 일 때 f(x)의 극한값은 존재하지 않는다. 같은 방법으로 임의의 정수 n에 대하여 x→n 일 때 f(x)의 극한값은 존재하지 않는다.

정의 3. (우방극한ㆍ좌방극한) 함수 f는 a<x<a+r을 만족하는 x의 집합에서 정의되어 있다 하자. x가 a의 오른쪽에서 가까와질 때 f(x)가 α에 가까와지면 α를 f(x)의 우방극한이라 하고

\[\lim_{x\to a+0}f(x)=\alpha\]

로 나타낸다.

같은 방법으로 함수 f가 a-r<x<a를 만족하는 x의 집합에서 정의되어 있고 x가 a의 왼쪽에서 가까와질 때 f(x)가 β에 가까와지면 β를 f(x)의 좌방극한이라 하고

\[\lim_{x\to a-0}f(x)=\beta\]

로 나타낸다.

x→a 일 때 f(x)의 극한값이 α이기 위한 필요충분조건은 두 조건

\[\begin{align}&(1)\ \lim_{x\to a+0}f(x)\ \text{및}\ \lim_{a\to a-0}f(x)\text{가 존재한다.}\\&(2)\ \lim_{x\to a+0}f(x)=\lim_{x\to a-0}f(x)=\alpha\end{align}\]

을 만족하는 것이다.

《문      제》

1. ε-δ법에 의하여 다음의 극한 값을 구하여라.

\[(1)\ \lim_{x\to0}2x\qquad(2)\ \lim_{x\to0}\frac{x^2-2x}{x}\qquad(3)\ \lim_{x\to2}\frac{5x^2-20}{x-2}\qquad(4)\ \lim_{x\to-1}\frac{x^3+x^2}{x+1}\]

<풀이>

(1) 임의의 ε>0가 주어지고 |f(x)|=2|x|<ε 이기 위해서는 |x|<ε/2 이다.

따라서 δ=ε/2라 하면 0<|x|<δ인 x에 대하여 |f(x)|<ε 이므로 \(\lim_{x\to0}f(x)=0\).

(2) 임의의 ε>0가 주어지고 x≠0 이면 |f(x)+2|=|x-2+2|=|x| 이므로 δ=ε라 하면 0<|x|<δ인 x에 대하여 |f(x)+2|<ε 이므로 \(\lim_{x\to0}f(x)=-2\).

(3) 임의의 ε>0가 주어지고 x≠2 이면 |f(x)-20|=|5x+10-20|=5|x-2| 이므로 δ=ε/5라 하면 0<|x-2|<δ인 x에 대하여 |f(x)-20|<ε 이므로 \(\lim_{x\to2}f(x)=20\).

(4) 임의의 ε>0가 주어지고 x≠1 이면 |f(x)-1|=|x²-1|=|(x-1)(x+1)|=|x-1||x+1|.

따라서 |f(x)-1|<ε 이기 위해서는 |x+1|<ε/|x-1|이면 된다. δ=1 이라 하면 |x|-1≤|x+1|<1(=δ)인 x에 대하여 |x|<2.

따라서 |x-1|≤|x|+1<2+1=3. 곧, ε/|x-1|>ε/3 이다.

δ=min{1, ε/3} 이고 0<|x+1|<δ인 x에 대하여 |f(x)-1|<ε 이므로 \(\lim_{x\to-1}f(x)=1\).

2. f(x)=[x]라 한다. n을 임의의 정수라 할 때 \(\lim_{x\to n+0}f(x)\) 및 \(\lim_{x\to n-0}f(x)\)를 각각 구하여라.

<풀이> [x]는 x를 넘지않는 최대 정수이므로 \(\lim_{x\to n+0}f(x)=n,\,\lim_{x\to n-0}f(x)=n-1\).

3. 함수 f는 다음과 같이 정의되어 있다.

\(\begin{cases}x>0\ \text{일 때}\ f(x)=1,\\x=0\ \text{일 때}\ f(x)=0,\\x<0\ \text{일 때}\ f(x)=-1.\end{cases}\)

이 때 \(\lim_{x\to+0}f(x)\) 및 \(\lim_{x\to-0}f(x)\)를 구하여라.

<풀이> \(\lim_{x\to+0}f(x)=1,\,\lim_{x\to-0}f(x)=-1\).

4. 함수 f(x)=x/|x|에 대하여 0의 우방극한과 좌방극한을 구하여라.

<풀이> x>0 일 때 f(x)=1, x<0 일 때 f(x)=-1 이므로

\(\lim_{x\to+0}f(x)=1,\,\lim_{x\to-0}f(x)=-1\).

5. \(\lim_{x\to a+0}f(x)=\alpha,\,\lim_{x\to a-0}f(x)=\beta\) 임을 ε-δ법을 사용하여 정의하여라.

<풀이>

우방극한 : 임의의 ε>0에 대하여 양수 δ가 정해지고 0<x-a<δ를 만족하는 모든 x에 대하여 |f(x)-α|<ε 이면 x→a+0 일 때 f(x)→α 이다.

좌방극한 : 임의의 ε>0에 대하여 양수 δ가 정해지고 0<a-x<δ를 만족하는 모든 x에 대하여 |f(x)-β|<ε 이면 x→a-0 일 때 f(x)→β 이다.

6. \(\lim_{x\to a}(mx+n)=ma+n\) 임을 증명하여라.

<풀이> 임의의 ε>0가 주어지고 |f(x)-(ma+n)|=m|x-a|<ε 이기 위해서는 |x-a|<ε/m 이다. 따라서 δ=ε/m 이면 0<|x-a|<δ인 x에 대하여 |f(x)-(ma+n)|<ε 이므로 x→a 일 때 f(x)→ma+n 이다.