변환행열 (Transformation Matrices)

개요(Introduction)

본 글은 변환행열 Q의 생성과 해석 측면에서 촛점을 맞춤으로써 이전 좌표변환 글을 보충하게 될 것이다. 좌표변환은 물체가 아닌 좌표축이 회전하는 것임을 다시 한번 강조한다.

사전복습(Quick Review)

변환행열 Q는 다음과 같이 벡터(vector)와 텐서(tensor)의 좌표변환에 사용된다(2등급 텐서를 1차 텐서, 4등급 텐서를 2차 텐서라고도 한다).

벡터                                  \({\bf v}'={\bf Q}\cdot{\bf v}\)

2등급(2nd rank) 텐서    \(\boldsymbol\sigma'={\bf Q}\cdot\boldsymbol\sigma\cdot{\bf Q}^T\)
4등급(4th rank) 텐서    \({\bf C}'={\bf Q}\cdot{\bf Q}\cdot{\bf C}\cdot{\bf Q}^T\cdot{\bf Q}^T\)

또한 텐서표기법으로 쓰면 ...

벡터                \(v'_i=\lambda_{ij}v_j\)
2등급 텐서    \(\sigma'_{mn}=\lambda_{mi}\lambda_{nj}\sigma_{ij}\)
4등급 텐서    \(C'_{mnop}=\lambda_{mi}\lambda_{nj}\lambda_{ok}\lambda_{pl}C_{ijkl}\)

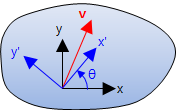
2차원에서 Q는

\[{\bf Q}=\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\]

여기서 θ는 변환전후 좌표축 간의 각도이다. 이것은 아래서 논의할 일반적인 3-D의 특별한 경우에 지나지 않는다.

변환행열의 성질(Transformation Matrix Properties) 변환행열은 아래의 2-D 벡터의 예에서 쉽게 알 수 있듯이 몇가지 특별한 성질이 있으며 3-D에도 동일하게 적용된다. 이 성질들은 만약 어떤 변환행열이 문제가 되었을 때 그것의 정확도를 검증하는데 유용하다. 변환행열이 이들 모든 항목을 통과하더라도 틀릴 수 있지만, 하나라도 만족하지 않으면 그것은 명백히 잘못된 것이다. ● Q의 행열식(determinant)은 1이다. ● Q의 전치행열(transpose)은 그의 역행열(inverse)이다. ● 임의의 행 또는 열과 그 자신과의 내적(dot product)은 1이다.      예 : \((i\cos\theta+j\sin\theta)\cdot(i\cos\theta+j\sin\theta)=1\) ● 임의의 행과 다른 행과의 내적은 0 이다.      예 : \((i\cos\theta+j\sin\theta)\cdot(-i\sin\theta+j\cos\theta)=0\) ● 임의의 열과 다른 열과의 내적은 0 이다.      예 : \((i\cos\theta-j\sin\theta)\cdot(i\sin\theta+j\cos\theta)=0\)

변환행열의 곱(Multiplication of Transformation Matrices) 위에서 변환행열의 임의의 두개의 다른 행 또는 열 간의 내적은 0 이고, 반면에 임의의 행 또는 열과 그 자신의 내적은 1 임에 주목한다. 이것은 행열과 텐서표기법으로 다음과 같이 쓸 수 있다. \[{\bf Q}\cdot{\bf Q}^T={\bf I}\qquad\text{그리고}\qquad\lambda_{ik}\lambda_{jk}=\delta_{ij}\] 이것은 또한 변환행열의 전치는 그의 역행열임을 보여준다.

3-D에서 Q의 일반적인 정의는 다음과 같다.

\[{\bf Q}=\begin{bmatrix}\cos(x',x)&\cos(x',y)&\cos(x',z)\\\cos(y',x)&\cos(y',y)&\cos(y',z)\\\cos(z',x)&\cos(z',y)&\cos(z',z)\end{bmatrix}\]

여기서 (x',x)는 x'와 x축 사이의 각도를 나타내고, (x', y)는 x'와 y축 사이의 각도를 나타낸다(이하 동일 규칙).

3-D로부터 2-D 축소(3-D Reduction to 2-D) 따라서 z-축에 대한 회전은 z'과 z 간의 각도가 0˚ 이기 때문에 cos(z',z)=1 이다. 반면에 cos(x',z)=cos(z',x)=0 이다. 왜냐하면 이들 축간의 각도는 90˚를 유지하기 때문이다. x'와 y 사이의 각도는 (90˚-θ), 그리고 cos(x',y)=cos(90˚-θ)=sinθ. 같은 방법으로 y'과 x 사이의 각도는 (90˚+θ), 그리고 cos(y',x)=cos(90˚+θ)=-sinθ. 이들을 모두 종합하면 \[{\bf Q}=\begin{bmatrix}\cos\theta&\sin\theta&0\\-\sin\theta&\cos\theta&0\\0&0&1\end{bmatrix}\] 여기서 3-D 변환행열 안에 2-D 행열이 포함되어 있음을 알 수 있다.

변환행열은 생성하고 해석하는 다른 방법은 다음과 같다.

\[\begin{bmatrix}\begin{pmatrix}x-comp\\of\ {\bf i}'\end{pmatrix}&\begin{pmatrix}y-comp\\of\ {\bf i}'\end{pmatrix}&\begin{pmatrix}z-comp\\of\ {\bf i}'\end{pmatrix}\\\begin{pmatrix}x-comp\\of\ {\bf j}'\end{pmatrix}&\begin{pmatrix}y-comp\\of\ {\bf j}'\end{pmatrix}&\begin{pmatrix}z-comp\\of\ {\bf j}'\end{pmatrix}\\\begin{pmatrix}x-comp\\of\ {\bf k}'\end{pmatrix}&\begin{pmatrix}y-comp\\of\ {\bf k}'\end{pmatrix}&\begin{pmatrix}z-comp\\of\ {\bf k}'\end{pmatrix}\end{bmatrix}\]

여기서 "x-comp of i'"은 i' 단위벡터(unit vector)의 x-성분(component)을 의미한다. 다른 말로 하면 "i' 단위행열의 x, y, z 좌표계 기준 첫번째 성분"이라 할 수 있다.

연속 회전 - 로우 규약(Successive Rotations -Roe Convention)

3-D 변환행열은 좌표축에 관한 일련의 연속적인 3번의 회전이라고 볼 수 있다. 회전축들의 조합이 임의의 순서로 선택될 수 있으므로 수많은 방법이 있을 수 있다. 하나의 많이 쓰이는 방법으로 소위 로우 규약(Roe convention)이 있다.

이것은 그림에서 보는바와 같이 (i) z-축을 중심으로 각도 ψ 만큼 회전한 후, (ii) 새로운 y-축(z를 중심으로 이미 회전한)을 중심으로 각도 θ 만큼 회전하고 마지막으로, (iii) 기울어진 z-축을 중심으로 두번째 Φ 만큼 회전하므로 이루어진다.

이 로우 규약은 한가지 단점에도 불구하고 매우 자주 사용된다. 그것은 θ=0 이면, ψ와 Φ 간의 구별이 어려워지며, 그 둘의 합만으로 구성된다.

\[\begin{split}{\bf Q}&=\begin{bmatrix}\cos\phi&\sin\phi&0\\-\sin\phi&\cos\phi&0\\0&0&1\end{bmatrix}\begin{bmatrix}\cos\theta&0&-\sin\theta\\0&1&0\\\sin\theta&0&\cos\theta\end{bmatrix}\begin{bmatrix}\cos\psi&\sin\psi&0\\-\sin\psi&\cos\psi&0\\0&0&1\end{bmatrix}\\&=\begin{bmatrix}\cos\psi\cos\theta\cos\phi-\sin\psi\sin\phi&\sin\psi\cos\theta\cos\phi+\cos\psi\sin\phi&-\sin\theta\cos\phi\\-\cos\psi\cos\theta\sin\phi-\sin\psi\cos\theta&-\sin\psi\cos\theta\sin\phi+\cos\psi\cos\phi&\sin\theta\sin\phi\\\cos\psi\sin\theta&\sin\psi\sin\theta&\cos\theta\end{bmatrix}\end{split}\]

회전각도들은 ψ, θ, Φ 순서로 적용되지만, 행열들은 반대순서 : Φ, θ, ψ로 쓰여진다는 것에 주의한다.

로우 각도 예제(Roe Angles Example) 위의 그림에서 ψ=60˚, θ=30˚, 및 Φ=45˚ 이다. 이 로우 각도들로부터 다음과 같은 좌표 변환행열을 얻는다. \[\begin{split}{\bf Q}&=\begin{bmatrix}\cos60^\circ\cos30^\circ\cos45^\circ-\sin60^\circ\sin45^\circ&\sin60^\circ\cos30^\circ\cos45^\circ+\cos60^\circ\sin45^\circ&-\sin30^\circ\cos45^\circ\\-\cos60^\circ\cos30^\circ\sin45^\circ-\sin60^\circ\cos45^\circ&-\sin60^\circ\cos30^\circ\sin45^\circ+\cos60^\circ\cos45^\circ&\sin30^\circ\sin^45^\circ\\\cos60^\circ\sin30^\circ&\sin60^\circ\sin30^\circ&\cos30^\circ\end{bmatrix}\\&=\begin{bmatrix}-0.3062&0.8839&-0.3536\\-0.9186&-0.1768&0.3536\\0.2500&0.4330&0.8660\end{bmatrix}\end{split}\]

역산 - 행열로부터 로우 각도 결정(Going In Reverse - Determining Roe Anlges from a Matrix)

변환행열이 주어지고 그 행열에 해당하는 로우 변환각도들을 알고 싶다고 하자.

\[{\bf Q}=\begin{bmatrix}q_{11}&q_{12}&q_{13}\\q_{21}&q_{22}&q_{23}\\q_{31}&q_{32}&q_{33}\end{bmatrix}\]

첫째로 가장 쉬운 단계는 \(q_{33}\) 성분을 이용하는 것이다. 그것은 단순히 θ의 코사인이므로, \(\theta={\rm Cos}^{-1}(q_{33})\) 이다.

두번째 단계로 다음과 같이 ψ를 결정한다.

\[{q_{32}\over q_{31}}={\sin\psi\sin\theta\over\cos\psi\sin\theta}={\sin\psi\over\cos\psi}=\tan\psi\]

따라서,

\[\phi={\rm Tan}^{-1}\left(q_{23}\over-q_{13}\right)\]

하지만 θ가 매우 작은 경우, sinθ 도 매우 작게 되어, sinθ가 포함되어 있는 \(q_{13},\,q_{23},\,q_{31}\) 및 \(q_{33}\)도 작아지게 된다. 이것은 반올림 오차(round-off errors)의 원인이 될 수 있다.

다행히도 이러한 경우(θ→0)에 대한 해결책은 ψ와 Φ를 서로 구별할 수 없다는 것에 있다. Φ를 0으로 둘 수 있으며, \(\psi={\rm Sin}^{-1}(q_{12})\)로 계산된다.

예제: 행열로부터 로우 각도 계산(Example: Roe Angles from Matrix) 앞의 예제의 행열을 가지고 거꾸로 계산한다. 먼저 θ를 결정하기 위해 \(q_{33}\) 항으로 시작한다. \[\theta={\rm Cos}^{-1}(q_{33})={\rm Cos}^{-1}(0.8660)=30^\circ\] θ가 0에 가깝지 않으므로, ψ와 Φ는 다음과 같이 계산된다. \[\begin{split}\psi&={\rm Tan}^{-1}\left(q_{32}\over q_{31}\right)={\rm Tan}^{-1}\left(0.4330\over0.2500\right)=60^\circ\\\phi&={\rm Tan}^{-1}\left(q_{23}\over-q_{13}\right)={\rm Tan}^{-1}\left(0.3536\over0.3536\right)=45^\circ\end{split}\]

임의의 축에 대한 회전(Rotation About An Axis)

변환된 좌표계의 방향을 명시하는 또 다른 방법은 회전축 벡터(rotation axis vector) \({\bf p}=(p_1,\,p_2,\,p_3)\)와 그 p축을 중심으로 회전각도 α를 사용하는 것이다.

이 경우 변환행열은 다음과 같이 쓰여 진다.

\[{\bf Q}=\cos\alpha{\bf I}+(1-\cos\alpha){\bf p}\otimes{\bf p}+\sin\alpha{\bf P}\]

여기서

\[{\bf P}=\begin{bmatrix}0&p_3&-p_2\\-p_3&0&p_1\\p_2&-p_1&0\end{bmatrix}\]

이 행열은 전개하면

\[{\bf Q}=\begin{bmatrix}\cos\alpha+(1-\cos\alpha)p_1^2&(1-\cos\alpha)p_1p_2+\sin\alpha p_3&(1-\cos\alpha)p_1p_3-\sin\alpha p_2\\(1-\cos\alpha)p_2p_1-\sin\alpha p_3&\cos\alpha+(1-\cos\alpha)p_2^2&(1-\cos\alpha)p_2p_3+\sin\alpha p_1\\(1-\cos\alpha)p_3p_1+\sin\alpha p_2&(1-\cos\alpha)p_3p_2-\sin\alpha p_1&\cos\alpha+(1-\cos\alpha)p_3^2\end{bmatrix}\]

통상 그렇듯이 윗 식은 텐서표기법으로 간결하게 쓸 수 있다.

\[Q_{ij}=\cos\alpha\delta_{ij}+(1-\cos\alpha)p_ip_j+\sin\alpha\epsilon_{ijk}p_k\]

p는 단위벡터라는 것에 유의한다. 다른 길이를 사용하면 잘못된 결과를 낳게된다.

로우 각도와 같이 주어진 변환행열 Q로부터 p와 α를 구할 수 있다. 첫번째 단계로 α를 결정한다. 이것은 행열의 대각합을 취함으로써 구해진다. 

\[\alpha={\rm Cos}^{-1}\left[{1\over2}\left\{\text{tr}({\bf Q})-1\right\}\right]\]

α가 결정되면, p의 성분들은 다음 식들로 계산된다.

\[p_1=\frac{q_{23}-q_{32}}{2\sin\alpha}\qquad p_2=\frac{q_{31}-q_{13}}{2\sin\alpha}\qquad p_3=\frac{q_{12}-q_{21}}{2\sin\alpha}\]

이 3개의 방정식은 텐서표기법으로 간편하게 요약된다.

\[p_i=\frac{\epsilon_{ijk}q_{jk}}{2\sin\alpha}\]

α=0 일 때는 p가 정의되지 않는다. 이것은 "만약 회전이 전제되지 않으면 회전축은 의미가 없다"는 것을 보여준다.

p와 α의 역산(Backing Out p and α) 앞의 로우 각도: ψ=60˚, θ=30˚, 및 Φ=45˚ 와 동일한 단일회전 p와 α를 결정하라. α에 대해서 풀면 \[\alpha={\rm Cos}^{-1}\left\{{1\over2}(-0.3062-0.1768+0.8660-1)\right\}=108^\circ\] p에 대해서 풀면 \[\begin{split}&p_1=\frac{0.3536-0.4330}{2\sin108^\circ}=-0.0417\\&p_2=\frac{0.2500+0.3536}{2\sin108^\circ}=0.3173\\&p_3=\frac{0.8839+0.9186}{2\sin108^\circ}=0.9475\end{split}\] 따라서 로우 각도 ψ=60˚, θ=30˚, 및 Φ=45˚ 는 p=(-0.0417, 0.3173, 0.9475)로 주어진 축을 중심으로 하는 108˚ 단일 회전과 동일하다.

역행열과 전치행열(Inverse and Transposes)

모든 좌표 변환행열은 다소 주목할 만한 성질을 가진다. - 그들의 전치행열은 역행열과 같다. 따라서 이 행열의 역행열을 구하는 것은 쉬운 일이다.

\[{\bf Q}^T={\bf Q}^{-1}\ \text{그러므로}\ {\bf Q}^T\cdot{\bf Q}={\bf Q}^{-1}\cdot{\bf Q}={\bf I}\]

전치행열과의 곱 예제(Transpose Product Example) 앞의 Q 행열을 그의 전치행열과 곱하면 단위행열임을 알 수 있고, 그러므로 그것의 전치행열은 역행열과 같아야 한다. \[\begin{align}{\bf Q}^T\cdot{\bf Q}&=\begin{bmatrix}-0.3062&-0.9186&0.2500\\0.8839&-0.1768&0.4330\\-0.3536&0.3536&0.8660\end{bmatrix}\begin{bmatrix}-0.3062&0.8839&-0.3536\\-0.9186&-0.1768&0.3536\\0.2500&0.4330&0.8660\end{bmatrix}\\&=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\end{align}\]