좌표변환 (Coordinate Transformation)
개요 (Introduction)
본 글에서는 좌표변환(coordinate transformation)을 다음 순서대로 다루게 된다: (i) 2-D 벡터, (ii) 2-D 텐서, (iii) 3-D 벡터, (iv) 3-D 텐서, 그리고 최종적으로 4등급 텐서(4th rank tensor) 변환에 대해 알아 본다.
좌변변환의 주요 관점은, 특히 3-D에서, 변환행열(transformation matrix)을 유도하는 것이다. 여기서는 소개만하고 변환행열 글에서 자세히 다루도록 한다.
본 글에서의 모든 좌표변환은 물체 자신은 고정된 채 좌표가 회전하는 것임을 하는 것이 매우 중요하다. 여기서 "물체"는 힘 또는 속도와 같은 벡터, 혹은 요소의 응력이나 변형률 같은 텐서가 될 수도 있다. 물체의 회전은 회전행열 글에서 다룬다.
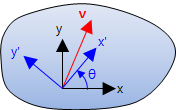
벡터의 2-D 좌표변환 (2-D Coordinate Transformation of Vectors)
아래와 같은 물체가 벡터를 가지고 있다고 하자. 하지만 좌표계(coordinate system)가 없이는 벡터를 기술할 방법이 없다. 그러므로 xy 좌표계가 그림과 같이 추가되면 이 벡터는 v=2i+9j와 같이 기술할 수 있다.
이제 청색으로 나타낸 회전 좌표계 x'y'을 도입한다. 이 새로운 좌표계는 원좌표계로부터 반시계 방향으로 θ 만큼 회전된 것이다. 이 벡터 자신은 변한게 전혀 없다는 점에 주의한다. 하지만 새로운 좌표계에서는 다른 값으로 기술된다. 이 경우, 벡터는 새로운 y'축보다 x'축에 좀 더 평행하게 근접하므로 i' 성분은 j' 성분보다 클 것이다.
이 2-D 벡터 변환 방정식은 i 성분을 \(v_x\), j 성분을 \(v_y\)로 두면
\[\begin{split}&v'_x=\ \ \,v_x\cos\theta+v_y\sin\theta\\&v'_y=-v_x\sin\theta+v_y\cos\theta\end{split}\]
이 식은 아래와 같이 생각하면 이해하기 쉽다.
● \(v_x\)가 y'축에 투영된 부분은 \(-v_x\sin\theta\) 이다.
● \(v_y\)가 y'축에 투영된 부분은 \(v_y\cos\theta\) 이다.
이 4개의 요인은 위의 변환 방정식의 4개의 항을 구성한다.
앞의 문제로 돌아가서 … θ=50˚ 이면\[\begin{split}&v'_x=\ \ \,2\cos50^\circ+9\sin50^\circ=8.18\\&v'_y=-2\sin50^\circ+9\cos50^\circ=4.25\end{split}\] \(v'_x\) 성분은 실제로 예상한 바와 같이 \(v'_y\) 보다 커졌음을 알 수 있다. |
변환행열 (Transformation Matirx)
변환 방정식은 행열을 이용하여 쓰고 계산하는 것이 휠씬 편리하다.
\[\begin{Bmatrix}v'_x\\v'_y\end{Bmatrix}=\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}=\begin{Bmatrix}v_x\\v_y\end{Bmatrix}\]
위의 방정식은 행열 표기법으로는 아래와 같이 쓰여진다.
\[{\bf v}'={\bf Qv}\]
여기서 Q는 통상적으로 변환행열을 나타내는 문자이다.
변환행열의 성질 (Transformation Matrix Properties) 변환행열은 2-D 벡터에서 쉽게 증명할 수 있는 몇가지 특이한 성질을 가지고 있는데 3-D의 경우도 똑같이 적용된다. 이 성질들은 문제 발생 시 변환행열의 정확도를 검증하는데 유용하다. 이들을 모두 통과했더라도 변환행열은 틀릴 수 있지만, 단 하나라도 만족하지 못하면 명백히 틀린 것이다.● Q의 행열식(determinant)은 1이다. |
두 좌표계 간 각도의 코사인, 즉 방향 코사인(direction cosine)에 기반하여 변환행열을 공식화하는 일반적인 방법이 있다(이것은 또한 3-D에도 적용된다). 이 변환행열은 다음과 같이 쓰여진다.
\[{\bf Q}=\begin{bmatrix}\cos(x',x)&\cos(x',y)\\\cos(y',x)&\cos(y',y)\end{bmatrix}\]
여기서 (x', x)는 x'와 x축 사이의 각도를 나타내고, (x', y)는 x'와 y축 사이의 각도 등을 나타낸다.
x'와 y 사이의 각도는 (90˚-θ) 이므로 cos(x', y)=cos(90˚-θ)=sinθ.
같은 방법으로 y'와 x 사이 각도는 (90˚+θ) 이므로 cos(y', x)=cos(90˚+θ)=-sinθ,
변환행열 공식화 (Transformation Matrix Formulation) 변환행열을 산출하는 또 다른 방법은 다음과 같다.\[{\bf Q}=\begin{bmatrix}\begin{pmatrix}{\rm {\bf i}'의}\\x-{\rm 성분}\end{pmatrix}&\begin{pmatrix}{\rm {\bf i}'의}\\y-{\rm 성분}\end{pmatrix}\\\begin{pmatrix}{\rm {\bf j}'의}\\x-{\rm 성분}\end{pmatrix}&\begin{pmatrix}{\rm {\bf j}'의}\\y-{\rm 성분}\end{pmatrix}\end{bmatrix}\] "i'의 x-성분"은 i' 단위벡터(unit vector)의 x-성분이라는 의미이다. 다른 말로 하면 "기존 xy 좌표계 기준 i' 단위벡터의 첫번째 성분"을 말한다. 요약하면 ● i'의 x-성분은 cosθ |
텐서 표기법 (Tensor Notation)
좌표변환을 텐서 표기법으로 쓰면 아래와 같다.
\[v'_i=\lambda_{ij}v_j\]
여기서 \(\lambda_{ij}\)는 변환행열 Q를 나타낸다. \(\lambda_{ij}\)는 다음과 같이 정의된다.
\[\lambda_{ij}=\cos(x'_i,x_j)\]
예를 들면, i=1 그리고 j=2 이면
\[\lambda_{12}=\cos(x'_1,x_2)=\cos(x',y)\]
\(\lambda_{ij}\)는 \(x'_i\)축과 \(x_j\) 축 사이 각도의 방향 코사인이다. 이 역시 3-D 경우에도 동일하게 적용된다.
변환행열의 곱 (Multiplication of Transformation Matrices) 위에서 변환행열의 서로 다른 행 또는 열 간의 내적은 0이고, 그 자신의 행 또는 열 간의 내적은 1임을 기억하자. 이것은 행열과 텐서 표기법으로 다음과 같이 쓸 수 있다. \[{\bf QQ}^T={\bf I}\qquad\qquad\lambda_{ik}\lambda_{jk}=\delta_{ij}\] 또한 위의 식은 변환행열의 전치행열(transpose)은 역행열(inverse)과 같다는 것을 보여준다. |
텐서의 2-D 좌표변환 (2-D Coordinate Transformation of Tensors)
2등급 텐서(2nd rank tensor)의 좌표변환은 벡터 변환 때와 동일한 Q 행열을 사용한다. 기존 xy 좌표계의 응력텐서 σ에서 신규 x'y' 좌표계의 σ'으로의 변환은 다음과 같이 행해진다.
\[\boldsymbol\sigma'={\bf Q}\boldsymbol\sigma{\bf Q}^T\]
행열로 전개해서 쓰면
\[\begin{bmatrix}\sigma'_{xx}&\sigma'_{xy}\\\sigma'_{xy}&\sigma'_{yy}\end{bmatrix}=\begin{bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\begin{bmatrix}\sigma_{xx}&\sigma_{xy}\\\sigma_{xy}&\sigma_{yy}\end{bmatrix}\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\]
이 행열들을 곱하면 다음 식들을 얻는다.
\[\begin{align}&\sigma'_{xx}=\sigma_{xx}\cos^2\theta+\sigma_{yy}\sin^2\theta+2\sigma_{xy}\sin\theta\cos\theta\\&\sigma'_{yy}=\sigma_{xx}\sin^2\theta+\sigma_{yy}\cos^2\theta-2\sigma_{xy}\sin\theta\cos\theta\\&\sigma'_{xy}=(\sigma_{yy}-\sigma_{xx})\sin\theta\cos\theta+\sigma_{xy}(\cos^2\theta-\sin^2\theta)\end{align}\]
이들 3개의 방정식은 미소요소에 작용하는 합력의 평형으로 유도된 2-D 응력변환(stress transform)과 정확히 일치한다. 또한 이것은 모어원으로 표현이 가능하다.
2-D 텐서 변환 예제 (2-D Tensor Transform Example) 기존 좌표계의 응력 텐서가 아래와 같다 하자. \[\boldsymbol\sigma=\begin{bmatrix}1&2\\2&3\end{bmatrix}\] 좌표계를 50˚ 회전하면 이 응력 텐서는 다음과 같이 쓸 수 있다. \[\begin{align}\begin{bmatrix}\sigma'_{xx}&\sigma'_{xy}\\\sigma'_{xy}&\sigma'_{yy}\end{bmatrix}&=\begin{bmatrix}\cos50^\circ&\sin50^\circ\\-\sin50^\circ&\cos50^\circ\end{bmatrix}\begin{bmatrix}1&2\\2&3\end{bmatrix}\begin{bmatrix}\cos50^\circ&-\sin50^\circ\\\sin50^\circ&\cos50^\circ\end{bmatrix}\\&=\begin{bmatrix}4.14&0.64\\0.64&-0.14\end{bmatrix}\end{align}\] 앞의 벡터 예제와 같이, 응력상태는 전혀 변한 것이 없다. 단지 좌표계가 다르기 때문에 행열의 값들이 다를 뿐이다. |
텐서 표기법 (Tensor Notation)
2등급 텐서의 좌표변환을 텐서 표기법으로 쓰면
\[\sigma'_{mn}=\lambda_{mi}\lambda_{nj}\sigma_{ij}\]
통상적으로 텐서 표기법은 그 과정에 있어서 특별한 통찰력을 준다. 이 경우는 람다의 첨자로부터 통찰력을 얻을 수 있다. 각 람다의 첨자는 σ'와 σ의 첨자 하나씩을 취하여 쌍을 이룬다. 이것은 텐서의 등급과 상관없이 적용된다.
3-D 벡터의 좌표변환 (3-D Coordinate Transforms of Vectors)
2-D에서의 많은 일반적인 방정식들이 3-D에도 역시 적용된다. 그 예로서 다음식이 포함된다.
\[{\bf v}'={\bf Qv}\qquad\qquad v'_i=\lambda_{ij}v_j\]
이제는 단지 상세한 것들이 다를 뿐이다. 이 벡터들은 z-성분을 가지고 있으므로 변환행열은 2×2가 아닌 3×3 이다.
\[\begin{align}&{\bf v}=\begin{Bmatrix}v_x\\v_y\\v_z\end{Bmatrix}\qquad{\rm 그리고}\qquad{\bf Q}=\begin{bmatrix}\cos(x',x)&\cos(x',y)&\cos(x',z)\\\cos(y',x)&\cos(y',y)&\cos(y',z)\\\cos(z',x)&\cos(z',y)&\cos(z',z)\end{bmatrix}\\&=\begin{bmatrix}(\rm{\bf i}'의 x성분)&(\rm{\bf i}'의 y성분)&(\rm{\bf i}'의 z성분)\\(\rm{\bf j}'의 x성분)&(\rm{\bf j}'의 y성분)&(\rm{\bf j}'의 z성분)\\(\rm{\bf k}'의 x성분)&(\rm{\bf k}'의 y성분)&(\rm{\bf k}'의 z성분)\end{bmatrix}\\&\begin{Bmatrix}v'_x\\v'_y\\v'_z\end{Bmatrix}=\begin{bmatrix}\cos(x',x)&\cos(x',y)&\cos(x',z)\\\cos(y',x)&\cos(y',y)&\cos(y',z)\\\cos(z',x)&\cos(z',y)&\cos(z',z)\end{bmatrix}\begin{Bmatrix}v_x\\v_y\\v_z\end{Bmatrix}\end{align}\]
3-D 텐서의 좌표변환 (3-D Coordinate Transforms of Tensors)
또 다시, 규칙은 변하지 않고, 단지 상세 항목들만 바꾸면 된다.
\[\boldsymbol\sigma'={\bf Q}\boldsymbol\sigma{\bf Q}^T\qquad\qquad\sigma'_{mn}=\lambda_{mi}\lambda_{nj}\sigma_{ij}\]
행열들을 풀어쓰면 다음식을 얻는다.
\[\begin{bmatrix}\sigma'_{xx}&\sigma'_{xy}&\sigma'_{xz}\\\sigma'_{xy}&\sigma'_{yy}&\sigma'_{yz}\\\sigma'_{xz}&\sigma'_{yz}&\sigma'_{zz}\end{bmatrix}=\begin{bmatrix}\cos(x',x)&\cos(x',y)&\cos(x',z)\\\cos(y',x)&\cos(y',y)&\cos(y',z)\\\cos(z',x)&\cos(z',y)&\cos(z',z)\end{bmatrix}\begin{bmatrix}\sigma_{xx}&\sigma_{xy}&\sigma_{xz}\\\sigma_{xy}&\sigma_{yy}&\sigma_{yz}\\\sigma_{xz}&\sigma_{yz}&\sigma_{zz}\end{bmatrix}\begin{bmatrix}\cos(x',x)&\cos(y',x)&\cos(z',x)\\\cos(x',y)&\cos(y',y)&\cos(z',y)\\\cos(x',z)&\cos(y',z)&\cos(z',z)\end{bmatrix}\]
4등급 텐서의 좌표변환 (Coordinate Transforms of 4th Rank Tensors)
후크의 법칙(Hooke's Law)에서 강성텐서(stiffness tensor)는 4등급 텐서, 즉 3×3×3×3 이다. 이것은 어느 한 변형률 성분 \(\epsilon_{kl}\)을 어느 한 응력 성분 \(\sigma_{ij}\)과 관련시키기 때문에 \(C_{ijkl}\)로 쓰여진다. 4등급 텐서의 좌표변환은 텐서 표기법으로 다음과 같이 쉽게 쓸 수 있다.
\[C'_{ijkl}=\lambda_{im}\lambda_{jn}\lambda_{ko}\lambda_{lp}C_{mnop}\]
이 텐서 방정식은 행열 표기법(matrix notation)으로 어떻게 쓸 수 있는지 보여준다.
\[{\bf C}'={\bf QQCQ}^T{\bf Q}^T\]
4등급 텐서 변환 예제 (4th Rank Tensor Transform Example)
아래 예제는 단일층 강제 벨트(single ply steel belt)의 강성 계산을 보여준다. θ는 수평축으로부터 케이블의 회전 각도이다. 아래 방정식이 어떻게 삼각함수의 4승을 포함하는지 주의 깊게 보면, 4개의 Q 행열이 사용된 것과 일치함을 알 수 있다.
층구조 상세(Lamina Description)
부품좌표계(Body Coordinates) : X, Y, Z
층구조 가정(Lamina Assumptions) :
2. 고무는 비압축성(incompressible)이다(ν=0.5).
3. 케이블은 비압축성이다(케이블 응력은 상당한 변형률을 발생시키기에는 매우 낮음).
4. 케이블 탄성계수 Ec≫고무 탄성계수 E
\[\epsilon_1=\frac{\sigma_1}{\nu_cE_c}\ \text{where}\ \nu_c=\text{volume fraction of cable}\]
가정에 의해 재료 좌표계 기준의 응력-변형률 관계는 다음과 같다.
\[\boldsymbol\epsilon={\bf S}\boldsymbol\sigma=\begin{Bmatrix}\epsilon_1\\\epsilon_2\\\epsilon_3\end{Bmatrix}=\begin{bmatrix}S_{11}&S_{12}&0\\S_{12}&S_{22}&0\\0&0&S_{66}\end{bmatrix}\begin{Bmatrix}\sigma_1\\\sigma_2\\\sigma_3\end{Bmatrix}\]
\[\text{여기서 }S_{11}={1\over\nu_cE_c},\ S_{12}=0,\ S_{22}=\frac{1-\nu^2}{E}\left({P-D\over P}\right),\ S_{66}=\frac{2(1+\nu)}{E}\left(P-D\over P\right)\]
이 층구조의 응력-변형률 관계는 좌표변환을 통하여 부품 좌표계 기준으로 나타낼 수 있다. 그 과정을 행열 표기법으로 다음과 같이 쓸 수 있다.
\[\boldsymbol\epsilon'={\bf T}\boldsymbol\epsilon={\bf TS}\boldsymbol\sigma={\bf TST}^T\boldsymbol\sigma'=\overline{\bf S}\boldsymbol\sigma\]
\[\text{여기서 }{\bf T}=\begin{bmatrix}\cos^2\theta&\sin^2\theta&-\sin\theta\cos\theta\\\sin^2\theta&\cos^2\theta&\sin\theta\cos\theta\\\sin\theta\cos\theta&-\sin\theta\cos\theta&\cos^2\theta-\sin^2\theta\end{bmatrix},\ \overline{\bf S}=\begin{bmatrix}\overline{S}_{11}&\overline{S}_{12}&\overline{S}_{16}\\\overline{S}_{12}&\overline{S}_{22}&\overline{S}_{26}\\\overline{S}_{16}&\overline{S}_{26}&\overline{S}_{66}\end{bmatrix}\]
부품 좌표계 기준으로 변환된 강성행열의 각 성분을 전개하면
\[\begin{split}\overline{S}_{11}&=S_{11}\cos^4\theta+(2S_{12}+S_{66})\sin^2\theta\cos^2\theta+S_{22}\sin^4\theta\\&=\frac{\cos^4\theta}{\nu_cE_c}+\frac{1+\nu}{E}\left(P-D\over P\right)\sin^2\theta\left\{2-(1+\nu)\sin^2\theta\right\}\\\overline{S}_{12}&=S_{12}(\sin^4\theta+\cos^4\theta)+(S_{11}+S_{22}-S_{66})\sin^2\theta\cos^2\theta\\&=\frac{\sin^2\theta\cos^2\theta}{v_cE_c}-\frac{1+\nu}{E}\left(P-D\over P\right)\sin^2\theta\cos^2\theta(1+\nu)\\\overline{S}_{22}&=S_{11}\sin^4\theta+(2S_{12}+S_{66})\sin^2\theta\cos^2\theta+S_{22}\cos^4\theta\\&=\frac{\sin^4\theta}{\nu_cE_c}+\frac{1+\nu}{E}\left(P-D\over P\right)\cos^2\theta\left\{2-(1+\nu)\cos^2\theta\right\}\\\overline{S}_{16}&=(2S_{11}-2S_{12}-S_{66})\sin\theta\cos^3\theta-(2S_{22}-2S_{12}-S_{66})\sin^3\theta\cos\theta\\&=\frac{2\sin\theta\cos^3\theta}{\nu_cE_c}-\frac{1+\nu}{E}\left(P-D\over P\right)\sin2\theta\left\{1-(1+\nu)\sin^2\theta\right\}\\\overline{S}_{26}&=(2S_{11}-2S_{12}-S_{66})\sin^3\theta\cos\theta-(2S_{22}-2S_{12}-S_{66})\sin\theta\cos^3\theta\\&=\frac{2\sin^3\theta\cos\theta}{\nu_cE_c}-\frac{1+\nu}{E}\left(P-D\over P\right)\sin2\theta\left\{1-(1+\nu)\cos^2\theta\right\}\\\overline{S}_{66}&=2(2S_{11}+2S_{22}-4S_{12}-S_{66})\sin^2\theta\cos^2\theta+S_{66}(\sin^4\theta+\cos^4\theta)\\&=\frac{\sin^22\theta}{\nu_cE_c}+\frac{1+\nu}{E}\left(P-D\over P\right)\left\{2-(1+\nu)\sin^22\theta\right\}\end{split}\]
이 과정을 거쳐 각 변형률 성분을 응력에 대해 표시하면 아래와 같다. 유한 케이블 탄성계수(finite cable modulus) 및 각 변형률에서 케이블과 고무의 각 응력별 기여도에 주목한다. 고무의 기여도는 (P-D)/P로 스케일 되었다.
\[\begin{split}\epsilon_x=&\frac{\cos^2\theta}{\nu_cE_c}(\sigma_x\cos^2\theta+\sigma_y\sin^2\theta+2\tau_{xy}\sin\theta\cos\theta)+\\&\frac{1+\nu}{E}\left(P-D\over P\right)\left[\sigma_x\sin^2\theta\left\{2-(1-\nu)\sin^2\theta\right\}-\sigma_y(1+\nu)\sin^2\theta\cos^2\theta-\tau_{xy}\sin2\theta\left\{1-(1+\nu)\cos^2\theta\right\}\right]\\\epsilon_y=&\frac{\sin2\theta}{\nu_cE_c}(\sigma_x\cos^2\theta+\sigma_y\sin^2\theta+2\tau_{xy}\sin\theta\cos\theta)+\\&\frac{1+\nu}{E}\left(P-D\over P\right)\left[\sigma_y\cos^2\theta\left\{2-(1+\nu)\cos^2\theta\right\}-\sigma_x(1+\nu)\sin^2\theta\cos^2\theta-\tau_{xy}\sin2\theta\left\{1-(1+\nu)\cos^2\theta\right\}\right]\\\epsilon_{xy}=&\frac{\sin2\theta}{\nu_cE_c}(\sigma_x\cos^2\theta+\sigma_y\sin^2\theta+2\tau_{xy}\sin\theta\cos\theta)+\\&\frac{1+\nu}{E}\left(P-D\over P\right)\left[-\sigma_x\sin2\theta\left\{1-(1+\nu)\sin^2\theta\right\}-\sigma_y\sin2\theta\left\{1-(1+nu)\cos^2\theta\right\}-\tau_{xy}\left\{2-(1+\nu)\sin^22\theta\right\}\right]\end{split}\]
아래 그림의 벨트 변수들은 현대 레디얼 타이어 벨트(radial tire belt)의 전형적인 것들이다. 가용벨트 각도 범위에 대한 탄성계수 변화를 보여준다.
 |
| 층 탄성계수 vs 벨트 케이블 각도 |





댓글
댓글 쓰기