연속 방정식 (Continuity Equation)

연속 방정식은(continuity equation)은 오일러 분석(Euler analysis)에서 질량보존을 만족시킨다. t=0 에서 유체 입자의 위치를 모르기 때문에 라그란지 기술법(Lagrangian)이 불가하므로 이 방정식은 고전 유체역학에서 근간이 된다.

질량보존 (Conservation of Mass)

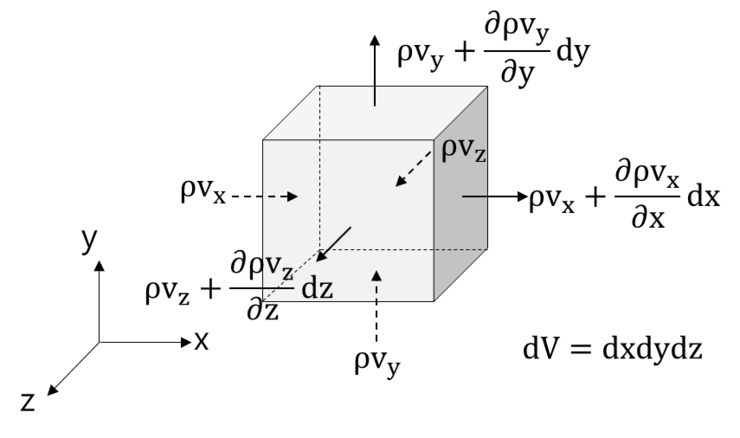
연속 방정식은 검사체적에 유입과 유출되는 질량 유속의 총합계로 전개되며, 질량의 변화율은 순수 유입량과 같다고 설정한다. 이를 보여주기 위해 아래 그림과 같은 미소 체적을 생각한다.

미소 검사체적의 유출과 유입되는 모든 질량유속을 같게 놓으면 다음식을 얻는다.

\[\begin{split}&\rho v_xdydz+\rho v_ydxdz+\rho v_zdxdy-\left(\rho v_x+\frac{\partial\rho v_x}{\partial x}dx\right)\\&-\left(\rho v_y+\frac{\partial\rho v_y}{\partial y}dy\right)-\left(\rho v_z+\frac{\partial\rho v_z}{\partial z}dz\right)=\frac{\partial}{\partial t}(\rho dxdydz)\end{split}\]

중복항을 삭제하고 dxdydz로 나누고 정리하면

위의 식은 행열과 텐서표기법으로 간단하게 쓸 수 있다.

\[\frac{\partial\rho}{\partial t}+\nabla\cdot(\rho{\bf v})=0\qquad\frac{\partial\rho}{\partial t}+(\rho v_i)_{,i}=0\]

유동이 정상상태(steady state)라면 시간미분항이 삭제되므로

\[\nabla\cdot(\rho{\bf v})=0\qquad(\rho v_i)_{,i}=0\]

비압축성(incompressibility) 유동이면 ρ=상수 이므로

\[\nabla\cdot{\bf v}=0\qquad v_{i,i}=0\]

위의 결과를 풀어쓰면

\[\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}={\rm tr}({\bf D})=0\]

전미분 (Material Derivative)    연속방정식의 발산항에 적(積)의 미분법을 적용하면 밀도에 대한 전미분, dρ/dt를 포함하여 나타낼 수 있다. \[\frac{\partial\rho}{\partial t}+{\bf v}\cdot\nabla\rho+\rho(\nabla\cdot{\bf v})=\frac{d\rho}{dt}+\rho(\nabla\cdot{\bf v})=0\]

연속방정식 적용 예 (Continuity Equation Example)    아래와 같이 유로가 좁아지면 유속이 빨라진다는 것을 직관적으로 알 수 있다. 연속방정식으로도 설명이 가능하다. 2-D 연속방정식을 생각하면 다음과 같다. \[\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}=0\] 유속의 y성분, \(v_y\)를 보면 y>0 영역에서는 유로가 점점 좁아지므로 \(v_y<0\) 이다. 반대로 y<0 이면 \(v_y>0\) 이다. 전체적으로 \((\partial v_y/\partial y)<0\)이 된다. 연속방정식에서 두개의 편미분항의 합이 '0'이 되어야하므로 \((\partial v_x/\partial x)>0\). 이것은 결국 유속이 증속되어야함을 의미한다.

출처 http://www.continuummechanics.org