응력 변환 (Stress Transformation)
2-D 응력 좌표 변환 (coordinate transforms)
좌표변환은 물체는 그대로 있고 좌표축이 회전한 경우이다. 주로 응력의 주방향(principal directions)을 찾는데 활용된다.
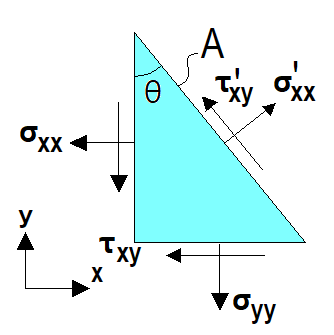
x, y 방향 힘의 평형은 다음과 같다.
\(\begin{split}\sigma_{xx}A\cos\theta+\tau_{xy}A\sin\theta&=\sigma'_{xx}A\cos\theta-\tau'_{xy}A\sin\theta\\\tau_{xy}A\cos\theta+\sigma_{yy}A\sin\theta&=\sigma'_{xx}A\sin\theta+\tau'_{xy}A\cos\theta\end{split}\)
면적 A를 소거하고 미지수 \(\sigma'_{xx},\,\tau'_{xy}\) 및 θ+90˚ 면수직응력 \(\sigma'_{yy}\)를 구하면
\(\begin{split}\sigma'_{xx}&=\sigma_{xx}\cos^2\theta+\sigma_{yy}\sin^2\theta+2\tau_{xy}\sin\theta\cos\theta\\\sigma'_{yy}&=\sigma_{xx}\sin^2\theta+\sigma_{yy}\cos^2\theta-2\tau_{xy}\sin\theta\cos\theta\\\tau'_{xy}&=\left(\sigma_{yy}-\sigma_{xx}\right)\sin\theta\cos\theta+\tau_{xy}\left(\cos^2\theta-\sin^2\theta\right)\end{split}\)
행렬 표기법으로 쓰면
\(\begin{bmatrix}\sigma'_{xx}&\tau'_{xy}\\\tau'_{yx}&\sigma'_{yy}\end{bmatrix}=\begin{bmatrix}\ \ \cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\begin{bmatrix}\sigma_{xx}&\tau_{xy}\\\tau_{yx}&\sigma_{yy}\end{bmatrix}\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\ \ \cos\theta\end{bmatrix}\)
앞 행렬을 Q로 쓰면 뒷 행렬은 그의 전치행렬이므로 다음과 같다.
\({\boldsymbol\sigma'}={\bf Q}\ \boldsymbol\sigma\ {\bf Q}^T\)
[예제] 응력텐서 σ가 기준좌표계에서 다음과 같을 때 좌표계가 50˚ 회전했을 때 응력 텐서 σ'는
\(\begin{align}{\boldsymbol\sigma}&=\begin{bmatrix}1&2\\2&3\end{bmatrix}\\&=\begin{bmatrix}\ \ \cos50^\circ&\sin50^\circ\\-\sin50^\circ&\cos50^\circ\end{bmatrix}\begin{bmatrix}1&2\\2&3\end{bmatrix}\begin{bmatrix}\cos50^\circ&-\sin50^\circ\\\sin50^\circ&\ \ \cos50^\circ\end{bmatrix}=\begin{bmatrix}4.143&\ \ \ 0.638\\0.638&-0.143\end{bmatrix}\end{align}\)
좌표변환을 텐서표기법(tensor notation)으로 쓰면
\(\sigma'_{mn}=Q_{mi}Q_{nj}\sigma_{ij}\)
3-D 응력 좌표 변환 (coordinate transforms)
좌표축이 추가되었을뿐 원칙은 2-D와 동일하다.
\({\boldsymbol\sigma'}={\bf Q}\ \boldsymbol\sigma\ {\bf Q}^T\quad\sigma'_{mn}=Q_{mi}Q_{nj}\sigma_{ij}\quad Q_{ij}=\cos(x'_i,\, x_j )\)
행렬을 풀어 쓰면
회전 변환 (Rotations)
회전 변환은 좌표축을 유지하면서 물체를 회전한 경우이다. 회전 행렬 R은 극좌표 분해(polar decomposition)로부터 계산된다.
응력텐서의 회전은
\({\boldsymbol\sigma'}={\bf R}\ \boldsymbol\sigma\ {\bf R}^T\)
2-D에서 회전행렬은 변환행렬의 전치(\({\bf R}={\bf Q}^T\))이므로 각도 θ 만큼 강체 회전의 경우
\(\begin{bmatrix}\sigma'_{xx}&\tau'_{xy}\\\tau'_{yx}&\sigma'_{yy}\end{bmatrix}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\ \ \cos\theta\end{bmatrix}\begin{bmatrix}\sigma_{xx}&\tau_{xy}\\\tau_{yx}&\sigma_{yy}\end{bmatrix}\begin{bmatrix}\ \ \cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}\)
변환 후 각 응력성분을 풀어 쓰면
\(\begin{align}\sigma'_{xx}&=\sigma_{xx}\cos^2\theta+\sigma_{yy}\sin^2\theta-2\tau_{xy}\sin\theta\cos\theta\\\sigma'_{yy}&=\sigma_{xx}\sin^2\theta+\sigma_{yy}\cos^2\theta+2\tau_{xy}\sin\theta\cos\theta\\\tau'_{xy}&=\left(\sigma_{xx}-\sigma_{yy}\right)\sin\theta\cos\theta+\tau_{xy}\left(\cos^2\theta-\sin^2\theta\right)\end{align}\)
3-D에서는
\(\begin{bmatrix}\sigma'_{xx}&\tau'_{xy}&\tau'_{xz}\\\tau'_{yx}&\sigma'_{yy}&\tau'_{yz}\\\tau'_{zx}&\tau'_{zy}&\sigma'_{zz}\end{bmatrix}=\begin{bmatrix}R_{11}&R_{12}&R_{13}\\R_{21}&R_{22}&R_{23}\\R_{31}&R_{32}&R_{33}\end{bmatrix}\begin{bmatrix}\sigma_{xx}&\tau_{xy}&\tau_{xz}\\\tau_{yz}&\sigma_{yy}&\tau_{yz}\\\tau_{zx}&\tau_{zy}&\tau_{zz}\end{bmatrix}\begin{bmatrix}R_{11}&R_{21}&R_{31}\\R_{12}&R_{22}&R_{32}\\R_{13}&R_{23}&R_{33}\end{bmatrix}\)
[예제] 위의 좌표계 변환 예제를 이번에는 각도 50˚의 강체회전에 적용한다.
\({\boldsymbol\sigma'}=\begin{bmatrix}\cos50^\circ&-\sin50^\circ\\\sin50^\circ&\ \ \cos50^\circ\end{bmatrix}\begin{bmatrix}1&2\\2&3\end{bmatrix}\begin{bmatrix}\ \ \cos50^\circ&\sin50^\circ\\-\sin50^\circ&\cos50^\circ\end{bmatrix}=\begin{bmatrix}\ \ 0.204&-1.332\\-1.332&\ \ 3.796\end{bmatrix}\)
좌표 및 회전 역변환 (Transforming and rotating back)
좌표 변환식 양변의 앞에 \({\bf Q}^T\), 뒤에 \({\bf Q}\)를 곱하면 \({\bf Q}^T={\bf Q}^{-1}\) 이므로
\({\bf Q}^T\ {\boldsymbol\sigma'}\ {\bf Q}={\bf Q}^T\ {\bf Q}\ \boldsymbol\sigma\ {\bf Q}^T\ {\bf Q}=\boldsymbol\sigma\)
같은 방법으로 물체가 회전 후 원래 각도로 복귀하는 변환은
\(\boldsymbol\sigma={\bf R}^T\ \boldsymbol\sigma'\ {\bf R}\)



댓글
댓글 쓰기