변형구배 (Deformation Gradient)
변형구배는 응력을 유발시키는 변형(deformation)으로부터 병진(translation) 및 회전(rotation)의 강체 운동(rigid body motion)을 분리하는데 쓰인다.
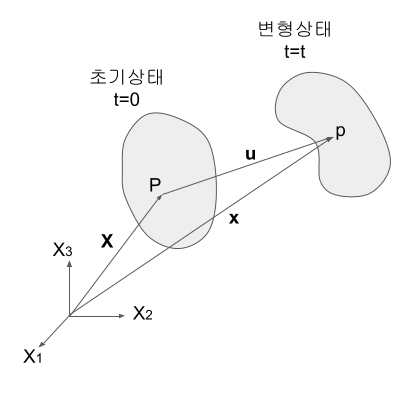
연속체 역학(continuum mechanics)의 규약에 따라 벡터 X는 변형전 초기 상태(undeformed reference configuration)를 그리고 x는 변형 후 현재 상태(deformed current configuration)를 정의한다.
변형구배 F는 변형후 x 벡터 각 성분의 초기 X 벡터 각 성분에 대한 도함수이다. x=x(X) 로 두면
\[F_{ij}=x_{i,j}=\frac{\partial x_i}{\partial X_j}=\begin{bmatrix}\frac{\partial x_1}{\partial X_1}&\frac{\partial x_1}{\partial X_2}&\frac{\partial x_1}{\partial X_3}\\\frac{\partial x_2}{\partial X_1}&\frac{\partial x_2}{\partial X_2}&\frac{\partial x_2}{\partial X_3}\\\frac{\partial x_3}{\partial X_1}&\frac{\partial x_3}{\partial X_2}&\frac{\partial x_3}{\partial X_3}\end{bmatrix}\]
임의의 점의 변위 u는 다음과 같이 정의할 수 있다.
\[{\bf u}={\bf x}-{\bf X}\]
위의 식으로부터 x=X+u 이므로
\[{\bf F}=\frac{\partial}{\partial\bf X}({\bf X}+{\bf u})=\frac{\partial\bf X}{\partial\bf X}+\frac{\partial\bf u}{\partial\bf X}={\bf I}+\frac{\partial\bf u}{\partial\bf X}\]
텐서 표기법으로 쓰면
\[F_{ij}=\delta_{ij}+u_{i,j}\]
\[\begin{align}&x=X+5\\&y=Y+2\end{align}\]
강체 회전의 예는 다음과 같다.
\[\begin{align}&x=X\cos\theta-Y\sin\theta\\&y=X\sin\theta+Y\cos\theta\end{align}\]
이 방정식은 물체를 z축을 중심으로 반시계 방향으로 회전시킨다. 이 경우 F는
\[{\bf F}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\]
회전은 변형이 존재하지 않지만 F의 값은 더이상 I가 아니다. 이것은 강체 회전이 변형과 변형률을 수반하는 것으로 잘못 해석될 수 있다. 이는 유한변형 역학(finite deformation mechanics)을 복잡하게 만드는 주된 요소이다. 회전(rotation)과 변형(deformation)이 같이 존재할 때는 이를 더욱 어렵게 만든다.
단순 변형 (Simple Deformation)
경우 1 - 신장 (Case 1 - Stretching)
x와 y 방향 늘음을 생각한다. 이 경우 아래 식은 x 방향으로는 100%, y 방향은 50%의 연신율을 나타낸다.
\[\begin{align}&x=2X\\&y=1.5Y\end{align}\]
변형구배는
\[{\bf F}=\begin{bmatrix}2&0\\0&1.5\end{bmatrix}\]
모든 비대각(off-diagonal) 성분은 영이라는 사실에 주목한다. \(F_{11}\)은 x 방향 신장을 나타내고, \(F_{22})는 y 방향 신장을 나타낸다.
경우 2 - 전단 (회전 수반) (Case 2 - Shear) (with Rotation)
아래 식은 위의 그림과 같은 정사각형의 전단을 나타낸다.
\[\begin{align}&x=X\\&y=0..5X+Y\end{align}\]
변형구배는
\[{\bf F}=\begin{bmatrix}1&0\\0.5&1\end{bmatrix}\]
경우 3 - 순수전단 (Case 3 - Pure Shear)
\[\begin{align}&x=X+0.5Y\\&y=0.5X+Y\end{align}\]
\[{\bf F}=\begin{bmatrix}1&0.5\\0.5&1\end{bmatrix}\]
영이 아닌 비대각(off-diagonal) 값은 전단이 존재함을 의미한다. F가 대칭이라는 사실은 회전이 수반되지 않음을 반영한다. 순(純) 회전이 영이라는 것은 동시에 사각형의 우하단은 시계 반대방향으로, 좌상단은 시계 방향으로 회전하려는 경향이 있다는 것으로부터 알 수 있다.
일반 변형 (General Deformation)
어느 물체가 정사각형에서 위의 그림과 같이 변형되었다고 생각하자. 이를 위한 식은 다음과 같고
\[\begin{align}&x=1.3X-0.375Y\\&y=0.75X+0.65Y\end{align}\]
해당 변형구배는
\[{\bf F}=\begin{bmatrix}1.3&-0.375\\0.75&0.65\end{bmatrix}\]
이 물체는 분명히 신장(stretched) 및 회전(rotated)되었다. 하지만 회전은 응력에 기여하지 않지만 변형은 기여한다. 따라서 응력과 변형 상태를 결정하기 위해서는 F로부터 두 거동을 분리하지 않으면 안된다.
극좌표 분해(polar decomposition)를 쓰면 이를 행할 수 있으나 여기서는 이해를 위해 다음 두 과정을 거친다.
첫 단계는 x 방향으로 50%를 신장시키고, y 방향으로 25%를 압축시킨다. 이는 X 기준 좌표계로부터 x' 중간 좌표계로의 변환식으로 표현된다.
\[\begin{align}&x'=1.5X\\&y'=0.75Y\end{align}\]
두번째 단계는 이 x'에 대한 표현식을 최종 x 좌표계로 회전시키는 것이다.
\[\begin{align}&x=x'\cos30^\circ-y'\sin30^\circ=1.3X-0.375Y\\&y=x'\sin30^\circ+y'\cos30^\circ=0.75X+0.65Y\end{align}\]
행열 표기법으로는
\[\begin{Bmatrix}x\\y\end{Bmatrix}=\begin{bmatrix}0.866&-0.5\\0.5&0.866\end{bmatrix}\begin{bmatrix}1.5&0\\0&0.75\end{bmatrix}\begin{Bmatrix}X\\Y\end{Bmatrix}\]
이고 변형구배는 회전 행열과 변형을 표현하는 대칭 행열의 곱으로 쓸 수 있다.
\[{\bf F}=\begin{bmatrix}1.3&-0.375\\0.75&0.65\end{bmatrix}=\begin{bmatrix}0.866&-0.5\\0.5&0.866\end{bmatrix}\begin{bmatrix}1.5&0\\0&0.75\end{bmatrix}\]
회전 행열은 30˚에 해당함을 쉽게 알 수 있다. 이 행열 곱은 일반적으로 다음과 같이 쓸 수 있다.
\[{\bf F}={\bf R}\cdot{\bf U}\]
여기서 R은 회전 행열(rotation matrix), U는 모든 응력, 변형률, 피로, 균열, 파단 등을 유발하는 오른쪽 신장 텐서(right stretch tensor)이다. 이 과정은 오른쪽에서 왼쪽으로 읽어야함에 유의한다. 즉, U를 먼저 적용하고 R은 그 다음이다.
이렇게 변형구배를 회전 행열과 신장 텐서로 분해하는 것을 극좌표 분해(polar decomposition)라 한다.
또는 다른 방법... (Or Alternatively)
\[\begin{align}&x'=X\cos30^\circ-Y\sin30^\circ\\&y'=X\sin30^\circ+Y\cos30^\circ\end{align}\]
그 다음 이 중간 구성식을 최종 변형 상태로 변형 시킨다.
\[\begin{align}&x=1.313x'+0.325y'\\&y=0.325x'+0.938y'\end{align}\]
비대각 값들은 물체가 신장/압축 외에 전단을 받고 있음을 나타낸다. 변형구배는 다음과 같이 쓸 수 있다.
\[{\bf F}=\begin{bmatrix}1.3&-0.375\\0.75&0.65\end{bmatrix}=\begin{bmatrix}1.313&0.375\\0.325&0.938\end{bmatrix}\begin{bmatrix}0.866&-0.5\\0.5&0.866\end{bmatrix}\]
이를 일반적으로 쓰면 다음과 같다.
\[{\bf F}={\bf V}\cdot{\bf R}\]
여기서 R은 동일한 회전 행열이고 V는 왼쪽 신장 텐서(left stretch tensor)이다. 이 역시 극좌표 분해(polar decomposition)이다.
V와 U의 관계(Relationship between V and U)
F=V·R=R·U 이고 양변 끝에 \({\bf R}^T\)를 곱하면
\[{\bf V}\cdot{\bf R}\cdot{\bf R}^T={\bf R}\cdot{\bf U}\cdot{\bf R}^T\]
한편 \({\bf R}\cdot{\bf R}^T={\bf I}\) 이므로 위의 식은 아래와 같이 V와 U의 관계를 보여준다.
\[{\bf V}={\bf R}\cdot{\bf U}\cdot{\bf R}^T\]
또는 U에 관하여 풀면 다음과 같다.
\[{\bf U}={\bf R}^T\cdot{\bf U}\cdot{\bf R}\]
V와 U의 관계 증명 (Verifying Relationship between V and U)
위의 일반 변형 예시에서
\[{\bf V}=\begin{bmatrix}1.313&0.325\\0.325&0.938\end{bmatrix}\qquad{\bf R}=\begin{bmatrix}0.866&-0.5\\0.5&0.866\end{bmatrix}\qquad{\bf U}\begin{bmatrix}1.5&0\\0&0.75\end{bmatrix}\]
\({\bf R}\cdot{\bf U}\cdot{\bf R}^T\)을 계산하면 아래와 같이 V와 같음을 알 수 있다.
\[\begin{split}{\bf R}\cdot{\bf U}\cdot{\bf R}^T&=\begin{bmatrix}0.866&-0.5\\0.5&0.866\end{bmatrix}\begin{bmatrix}1.5&0\\0&0.75\end{bmatrix}\begin{bmatrix}0.866&0.5\\-0.5&0.866\end{bmatrix}\\&=\begin{bmatrix}1.313&0.325\\0.325&0.938\end{bmatrix}\end{split}\]
서로 다른 강체 회전 시 V와 U (V and U for Different Rigid Body Rotations)
회전없이, x 방향 100% 신장된 물체에 대하여 변형구배와 극좌표 분해는
\[{\bf F}={\bf R}\cdot{\bf U}=\begin{bmatrix}\cos0^\circ&-\sin0^\circ\\\sin0^\circ&\cos0^\circ\end{bmatrix}\begin{bmatrix}2&0\\0&1\end{bmatrix}=\begin{bmatrix}2&0\\0&1\end{bmatrix}\]
한편 V·R 극좌표 분해는
\[{\bf F}={\bf V}\cdot{\bf R}=\begin{bmatrix}2&0\\0&1\end{bmatrix}\begin{bmatrix}\cos0^\circ&-\sin0^\circ\\\sin0^\circ&\cos0^\circ\end{bmatrix}=\begin{bmatrix}2&0\\0&1\end{bmatrix}\]
위의 결과와 같이 회전이 없을 때는 U, V 및 F는 모두 동일하다.
만약 물체가 원래 x 방향으로 100% 신장된 후에 90˚회전했다면 변형구배와 극좌표 분해는
또한 V·R 극좌표 분해는
\[{\bf F}={\bf V}\cdot{\bf R}=\begin{bmatrix}1&0\\0&2\end{bmatrix}\begin{bmatrix}\cos90^\circ&-\sin90^\circ\\\sin90^\circ&\cos90^\circ\end{bmatrix}=\begin{bmatrix}0&-1\\2&0\end{bmatrix}\]
신장 텐서, U는 위의 0˚와 90˚회전 예시에서 변하지 않았지만 F뿐만 아니라 V 신장 텐서는 변하였다. V의 성분들은 항상 회전 후의 변형에 해당된다.












댓글
댓글 쓰기