단순전단 (Simple Shear)

재료역학에서 단순전단은 요소의 마주보는 두 변이 평행하게 일정 거리를 유지하면서 서로에 대해 상대적으로 이동하는 변형이다.

이 변형은 강체 회전이 존재한다는 점에서 순수전단(pure shear)과는 다르다. 고무가 단순전단 변형을 할 때 응력-변형률 거동은 거의 선형관계가 된다. 봉의 비틀림은 단순전단을 받는 실제적인 예이다.

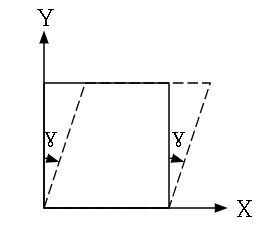
위의 그림과 같은 단순전단의 변형 후 상사 방정식(mapping equation)은 다음과 같다.

\[\begin{split}&x=X+\gamma Y\\&y=Y\end{split}\]

따라서 변형구배(deformation gradient)는 정의에 따라

\[\bf F=\begin{bmatrix}\frac{\partial x}{\partial X}&\frac{\partial x}{\partial Y}\\\frac{\partial y}{\partial X}&\frac{\partial y}{\partial Y}\end{bmatrix}=\begin{bmatrix}1&\gamma\\0&1\end{bmatrix}\]

강체회전이 존재하므로 위와 같이 변형구배는 비대칭 행열이 된다.

또한, 그림에서 요소가 변형하는 동안 고정되어 있는 밑변의 방향벡터 \({\bf e}_1\)이라 하고 \({\bf e}_1-{\bf e}_2\)면 상에서 변형이 일어난다고 하면 변형구배는 아래와 같이 쓸 수도 있다.

\[\begin{split}{\bf F}&={\bf I}+\gamma{\bf e}_1\otimes{\bf e}_2\\&=\begin{bmatrix}1&0\\0&1\end{bmatrix}+\gamma(1,0,0)\otimes(0,1,0)\\&=\begin{bmatrix}1&0\\0&1\end{bmatrix}+\gamma\begin{bmatrix}0&1\\0&0\end{bmatrix}\end{split}\]

위의 결과로부터 그린변형률(Green strain)을 구하면

\[\begin{split}{\bf E}&={1\over2}({\bf F}^T{\bf F}-{\bf I})\\&={1\over2}\left\{\begin{bmatrix}1&\gamma\\0&1\end{bmatrix}\begin{bmatrix}1&0\\\gamma&1\end{bmatrix}-\begin{bmatrix}1&0\\0&1\end{bmatrix}\right\}\\&={1\over2}\left\{\begin{bmatrix}1+\gamma^2&\gamma\\\gamma&1\end{bmatrix}-\begin{bmatrix}1&0\\0&1\end{bmatrix}\right\}\\&={1\over2}\begin{bmatrix}\gamma^2&\gamma\\\gamma&0\end{bmatrix}\end{split}\]

이것 역시 강체 회전이 발생하였으므로 비대각 성분(off-diagonal components)이 다름을 알 수 있다. 변형이 작을 경우 \(\gamma^2\to0\) 이므로 미소 변형률 텐서는

\[\boldsymbol\epsilon=\begin{bmatrix}\epsilon_{xx}&\epsilon_{xy}\\\epsilon_{yx}&\epsilon_{yy}\end{bmatrix}=\begin{bmatrix}0&{\gamma\over2}\\{\gamma\over2}&0\end{bmatrix}\]

여기서 \(\epsilon_{xy}=\epsilon_{yx}=\gamma/2\). 즉, 변형률 텐서의 전단성분은 공학 전단변형률(engineering shear strain)의 1/2임을 알 수 있다.