텐서 표기법 (Tensor Notation) -심화
본 글에서는 텐서 표기법을 좀 더 깊이 있게 알아본다. (처음 접하는 독자는 기본 과정 글을 참조한다.) 텐서 표기법의 강점은 하나의 텐서식으로 전체 방정식을 표현하는 데 있다. 이는 행렬 표기법으로는 불가능한 텐서항 간의 관계 파악과 조작을 가능하게 한다.
크로넥커 델타 및 좌표계 미분 (Kronecker Delta and Derivative of Axis Variables)
크로넥커 델타는 좌표계 변수의 그 자신에 대한 도함수와 관련된다. 직교좌표계의 경우는 간단히 아래와 같다. (원통좌표계는 '원통좌표계 벡터 변환' 글을 참조한다.)
\[\begin{split}&\frac{\partial x}{\partial x}=1\quad\frac{\partial x}{\partial y}=0\quad\frac{\partial x}{\partial z}=0\\&\frac{\partial y}{\partial x}=0\quad\frac{\partial y}{\partial y}=1\quad\frac{\partial y}{\partial z}=0\\&\frac{\partial z}{\partial x}=0\quad\frac{\partial z}{\partial y}=0\quad\frac{\partial z}{\partial z}=1\end{split}\]
이제 위의 식들은 텐서 표기법으로 아래와 같이 요약된다.
\[\frac{\partial x_i}{\partial x_j}=x_{i,j}=\delta_{ij}\]
예시 (Example)
크로넥커 델타와 좌표계 미분의 관계를 예를 들어 알아본다. 먼저 dy/dx 같은 도함수는 \((y_{\rm new}-y_{\rm old})\)를 \((x_{\rm new}-x_{\rm old})\)로 나눈 것이다. 다음은 점(2, 5, 9)을 기준으로 출발한다. 이제 x 좌표를 2에서 3까지 1 만큼 이동했다고 하자. 따라서 \((x_{\rm new}-x_{\rm old}=3-2=1)\).
하지만 y 좌표는 변한게 없으므로 그대로 5 이다. (직교좌표계에서는 각 방향이 독립적이다, 그러나 원통좌표계는 그렇지 않다.) 따라서 \((y_{\rm new}-y_{\rm old})=5-5=0\) 그리고 dy/dx=0.
반대로 dx/dx=1/1=1. 텐서 표기법으로는 확실히
\[\frac{dx_2}{dx_1}=x_{2,1}=\delta_{21}=0\quad\frac{dx_1}{dx_1}=x_{1,1}=\delta_{11}=1\]
크로넥커 델타의 곱셈 (Kronecker Delta Multiplication)
크로넥커 델타는 아래 예시와 같은 곱셈에 대한 특성 때문에 대입 연산자(substitution operator) 라는 별명으로 불리운다. 벡터 \(v_i\)에 \(\delta_{ij}\)를 곱하면 다음과 같다.
\[v_i\delta_{ij}=v_i\delta_{1j}+v_2\delta_{2j}+v_3\delta_{3j}\]
여기서 첨자 i는 하나의 항에서 두번 나오기 때문에 자동으로 1부터 3까지, \(v_i\)에서 한번씩, \(\delta_{ij}\)에서 한번씩 합하여 진다.(총합 규약)
이제 j에 대해서 임의로 j=3 이라 하자. 그러면 아래 식을 얻는다.
\[v_i\delta_{i3}=v_1\delta_{13}+v_2\delta_{23}+v_3\delta_{33}=v_3\]
\(\delta_{33}=1\) 이고 반면에 \(\delta_{13}=\delta_{23}=0\) 이기 때문에 결과는 간단히 \(v_3\) (j 대신 선택된 수)이다. 일반으로, \(v_i\delta_{ij}\)는 j의 어떤 값이 선택되는 항상 \(v_j\) 이다. 그러므로, 일반적이니 규약은
\[v_i\delta_{ij}=v_j\]
이 규약은 해당 항이 아무리 복잡해도 성립한다. 벡터의 외적항 \(\epsilon_{ijk}\omega_jr_k\)를 생각하자. 예를 들어 \(\delta_{im}\)를 곱하면
\[\delta_{im}\epsilon_{ijk}\omega_jr_k=\epsilon_{mjk}\omega_jr_k\]
위의 식은 순전히 순열 텐서(alternating tensor)에 i 대신 m을 대입한 결과와 같다.
스칼라 방정식 (Scalar Equations)
어떤 텐서항의 차수를 아는 것은 매우 중요하다. 사실 \(v_{i,i},\,a_ib_i,\,A_{ij}B_{ij},\) 그리고 \(\sigma_{ij}\epsilon_{ij}\) 같은 양들은 모두 스칼라 항이다. 이들은 또한 단일 스칼라 방정식이 될 수 있다. 요컨데, 선형 탄성 재질의 변형률 에너지 밀도(strain energy density) W는 다음식으로 주어지는 스칼라 양이다.
\[W={1\over2}\sigma_{ij}\epsilon_{ij}\]
위의 식에는 여러개의 첨자가 있지만 각각 두 번 반복되므로 총합규약에 의해 1부터 3까지 합하여 진다. 좌면 W에는 아무 첨자도 없으므로 명백히 스칼라 양이다.
벡터 방정식 (Vector Equation)
속도 벡터 \(v_i\)를 얻기 위한 각속도 벡터 \(\omega_j\)와 위치 벡터 \(r_k\)의 외적은 간단히 벡터 방식이다. (물론 이것은 단지 v=ω×r 이다.)
\[v_i=\epsilon_{ijk}\omega_jr_k\]
이 작은 텐서 방정식은 많은 것을 나타낸다. 우선 \(v_i\)항은 i=1, 2, 3의 각각에 대하여 하나의 식을 가지므로 위의 식은 하나가 아닌 3개의 식을 나타낸다. 둘째로 j와 k는 총합규약에 의해 합하여 지므로 각 3개의 식은 9개의 항을 포함한다. 하지만 \(\epsilon_{ijk}\)는 다음 항들만 남기고 대부분 영이다.
\[\begin{split}&v_1=\omega_2r_3-\omega_3r_2\\&v_2=\omega_3r_1-\omega_1r_3\\&v_3=\omega_1r_2-\omega_2r_1\end{split}\]
하나의 텐서 방정식은 많은 것을 내포하고 있다. 물론 텐서식이 외연적으로 3개의 식을 의미할 뿐 v=ω×r 또한 동일한 방정식이다.
2차 텐서 방정식 (2nd Order Tensor Equations)
통상적인 2차 텐서 방정식은 선형 탄성 재질의 응력과 변형률의 관계식인 후크의 법칙이다. 행렬 표기법으로 쓰면 다음과 같다.
\[\boldsymbol\epsilon={1\over E}\left\{(1+\nu)\boldsymbol\sigma-\nu{\bf I}{\rm tr}(\boldsymbol\sigma)\right\}\]
ε는 변형률 텐서
후크의 법칙을 텐서 표기법으로 쓰면
\[\epsilon_{ij}={1\over E}\left\{(1+\nu)\sigma_{ij}-\nu\delta_{ij}\sigma_{kk}\right\}\]
이 식의 각 항은 i와 j 첨자가 있으므로 분명히 2차이다. \(\sigma_{kk}\)는 k가 두번 나오므로 1부터 3까지 합이 되어 스칼라 양이다. 따라서 \(\sigma_{kk}\)는 σ의 대각합을 의미한다. 또 다른 주의점으로 \(\nu\delta_{ij}\sigma_{kk}\)항은 i=j 일 때만 영이 아니다. 이것은 수직응력과 변형률에 해당되면 전형적인 포아송 효과이다. 달리 말하면 i≠j 일 때는 \(\delta_{ij}\) 때문에 전체항이 영이 된다.
모든 행렬을 전개하면 다음 식을 얻는다.
\[\begin{bmatrix}\epsilon_{11}&\epsilon_{12}&\epsilon_{13}\\\epsilon_{21}&\epsilon_{22}&\epsilon_{23}\\\epsilon_{31}&\epsilon_{32}&\epsilon_{33}\end{bmatrix}={1\over E}\left\{(1+\nu)\begin{bmatrix}\sigma_{11}&\sigma_{12}&\sigma_{13}\\\sigma_{21}&\sigma_{22}&\sigma_{23}\\\sigma_{31}&\sigma_{32}&\sigma_{33}\end{bmatrix}-\nu\left(\sigma_{11}+\sigma_{22}+\sigma_{33}\right)\right\}\]
2 개의 자유 첨자가 있으므로 보통 3*3=9개의 방정식이 있어야 한다. 그러나 후크의 법칙은 모든 항이 대칭이므로 오로지 6개의 독립항만이 존재한다. 각 항들을 정리하면 아래와 같다.
\[\begin{split}&\epsilon_{11}={1\over E}\left\{\sigma_{11}-\nu\left(\sigma_{22}+\sigma_{33}\right)\right\}\qquad\epsilon_{12}={1+\nu\over E}\sigma_{12}\\&\epsilon_{22}={1\over E}\left\{\sigma_{22}-\nu\left(\sigma_{33}+\sigma_{11}\right)\right\}\qquad\epsilon_{31}={1+\nu\over E}\sigma_{31}\\&\epsilon_{33}={1\over E}\left\{\sigma_{33}-\nu\left(\sigma_{11}+\sigma_{22}\right)\right\}\qquad\epsilon_{23}={1+\nu\over E}\sigma_{23}\end{split}\]
또 다시 한 개의 텐서식에 많은 정보가 담겨 있는 것을 알 수 있다.
텐서 표기 대수법 - 후크의 법칙 역변환 (Tensor Notation Algebra - Inverting Hooke's Law)
지금까지는 텐서 표기법이 행렬 표기법을 능가하는 장점을 제공하지 못했다. 후크 법칙의 행렬 표기법도 텐서 표기법과 동일한 정보를 포함하고 있다. 하지만, 행렬 표기법 대비 텐서 표기법의 강력함은 텐서 방정식을 조작할 때 극명해 진다. 다음 예시는 응력의 함수인 변형률을 변형률의 함수인 응력으로 후크 법칙의 역함수를 유도하는 과정이다. 이런 역변환은 행렬 표기법에서는 거의 불가능하다.
앞의 후크 법칙의 텐서식으로부터 \(\sigma_{ij}\)에 관한 형태로 쉽게 바꿀 수 있다.
\[\sigma_{ij}={1\over1+\nu}\left(E\epsilon_{ij}+\nu\delta_{ij}\sigma_{kk}\right)\]
문제는 우변의 응력항 \(\sigma_{kk}\)가 아직 존재한다는 것이다. 이것은 양변에 \(\delta_{ij}\)를 다음과 같이 곱하므로서 극복할 수 있다.
\[\delta_{ij}\sigma_{ij}={1\over1+\nu}\left(E\delta_{ij}\epsilon_{ij}+\nu\delta_{ij}\delta_{ij}\sigma_{kk}\right)\]
이제부터 텐서 표기법의 몇몇 장점이 나타나기 시작한다. 첫째로 전체 방정식이 2차 텐서에서 더이상 자유첨자(free indices)가 없는 스칼라 방정식으로 변환되었다. 각 항은 i와 j가 두번씩 나오므로 1에서 3까지 더해지게 된다.
둘째로 \(\delta_{ij}\sigma_{ij}\)와 \(\delta_{ij}\epsilon_{ij}\)을 포함하는 항은 크로넥커 델타의 대입(substitution) 특성에 따라 단순화 할 수 있다. i=j 일 때만 \(\delta_{ij}=1\) 이므로
\[\begin{split}&\delta_{ij}\sigma_{ij}=\sigma_{kk}=\sigma_{11}+\sigma_{22}+\sigma_{33}\\&\delta_{ij}\epsilon_{ij}=\epsilon_{kk}=\epsilon_{11}+\epsilon_{22}+\epsilon_{33}\end{split}\]
마지막 \(\delta_{ij}\delta_{ij}\) 항은 3이다. 왜냐하면
\[\delta_{ij}\delta_{ij}=\delta_{kk}=\delta_{11}+\delta_{22}+\delta_{33}=1+1+1=3\]
따라서 스칼라 방정식은 다음과 같이 정리된다.
\[\sigma_{kk}={1\over1+\nu}\left(E\epsilon_{kk}+3\nu\sigma_{kk}\right)\]
이제 좌변과 우변의 \(\sigma_{kk}\)를 조합하면 다음식을 얻는다.
\[\sigma_{kk}={E\over1-2\nu}\epsilon_{kk}\]
위의 식을 원식에 대입하면 최종적으로 응력에 대한 변형률의 함수식을 얻는다.
\[\sigma_{ij}={E\over1+\nu}\left(\epsilon_{ij}+{\nu\over1-2\nu}\delta_{ij}\epsilon_{kk}\right)\]
ε-δ 항등식 (Epsilon-Delta Identity)
순열 텐서(alternating tensor)와 크로넥커 델타 사이에는 다음 항등식이 성립한다.
\[\begin{split}\epsilon_{ik}\epsilon_{lmn}&=\left|\begin{matrix}\delta_{il}&\delta_{im}&\delta_{in}\\\delta_{jl}&\delta_{jm}&\delta_{jn}\\\delta_{kl}&\delta_{km}&\delta_{kn}\end{matrix}\right|\\&=\delta_{il}\left(\delta_{jm}\delta_{kn}-\delta_{jn}\delta_{km}\right)+\delta_{im}\left(\delta_{jn}\delta_{kl}-\delta_{jl}\delta_{kn}\right)+\delta_{in}\left(\delta_{jl}\delta_{km}-\delta_{jm}\delta_{kl}\right)\end{split}\]
이 항등식의 양변에 \(\delta_{il}\)을 곱하면 유용한 다음식을 얻을 수 있다.
\[\epsilon_{ijk}\epsilon_{imn}=\delta_{jm}\delta_{kn}-\delta_{jn}\delta_{km}\]
이 식은 4개의 자유 첨자, j, k, m 그리고 n이 있으므로 4차 텐서식이다. 우변에 첨자 i는 두번 반복되므로 1부터 3까지의 총합규약이 적용된다.
위의 항등식은 보통 외적과 관련된 항에 순열 텐서가 있을 경우 사용된다. 이 식을 활용할 때 이점은 순열 텐서가 크로넥커 델타로 변환되면 대입 특성(substitution property)을 이용하여 방정식을 단순화할 수 있다는 것이다.
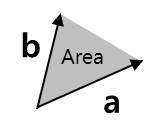
ε-δ 항등식 예제 1 (First Epsilon-Delta Identity Example)
삼각형의 면적은 양변 벡터의 외적으로 주어진다. 위의 항등식을 활용하면 아래와 같이 내적에 관한 식으로 변환할 수 있다.
ε-δ 항등식 예제 2 (Second Epsilon-Delta Identity Example)
다음 항등식을 증명하여라. 단, 여기서 v는 벡터이다.
\[\nabla\times(\nabla\times{\bf v})=\nabla(\nabla\cdot{\bf v})-\nabla^2{\bf v}\]
좌변 외적항을 순열 텐서를 이용하여 텐서 표기법으로 나타낸 다음 ε-δ 항등식을 활용하여 전재한다. 그 다음 크로넥커 델타의 대입 특성을 소거하면 우변과 동일한 식이 된다.
\[\begin{split}\epsilon_{mni}\epsilon_{ijk}v_{k,jn}&=\left(\delta_{mj}\delta_{nk}-\delta_{mk}\delta_{jn}\right)v_{k,jn}\\&=\delta_{mj}\delta_{nk}v_{k,jn}-\delta_{mk}\delta_{jn}v_{k,jn}\\&=v_{k,mk}-v_{m,nn}\\&=\left(v_{k,k}\right)_{,m}-\left(v_m\right)_{,nn}\\&=\nabla(\nabla\cdot{\bf v})-\nabla^2{\bf v}\end{split}\]
댓글
댓글 쓰기