축하중 부정정 구조의 강성법 (Stiffness Method)
 |
| 그림 1 정적 부정정 봉 (강성법 해석) |
강성법을 설명하게 위해 강체 지지부 사이의 균일단면 봉을 해석해 본다(그림 1a). Ra와 Rb는 지지부 반력들을 의미한다. 이 방법에서는 봉의 두 부분 연결부 C점의 수직변위 δc를 미지수로 취한다. 봉의 상하부 수직력 Ra와 Rb는 다음과 같이 δc의 항으로 표현할 수 있다.
\[R_a={EA\over a}\delta_c\qquad R_b={EA\over b}\delta_c\qquad\cdots(1)\]
이 방정식들에서 δc는 아래방향이 양으로 가정하여, 봉의 상부는 인장 그리고 하부는 압축을 받도록 하였다.
\[R_a+R_b={EA\over a}\delta_c+{EA\over b}\delta_c=P\]
\[\delta_c={Pab\over EAL}\]
(a+b=L 이므로). δc를 알게 되었으므로, 이제 식 (1)로부터 Ra와 Rb를 구할 수 있다.
\[R_a={Pb\over L}\qquad R_b={Pa\over L}\]
이 결과들은 당연히 하중법(유성법)으로 유도한 것들과 동일하다.
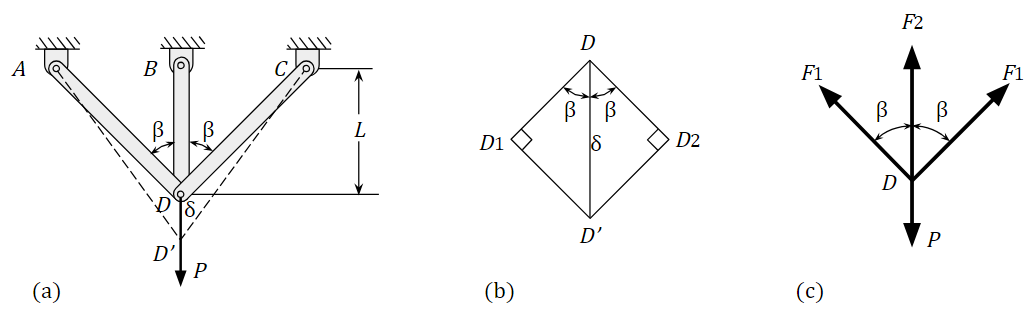 |
| 그림 2 정적 부정정 트러스 (강성법 해석) |
강성법의 두번째 설명으로 그림 2a와 같은 평면 트러스 해석을 생각한다(하중법에 있는 것과 동일한 트러스이다). 수직봉의 길이는 L 이고, 경사봉은 L/cosβ, 그리고 세개의 모든 봉들은 동일한 축강성 EA를 갖는다. 수직력 P가 연결부 D에 작용한다. 따라서 트러스와 하중이 대칭이므로 연결부 D의 수평방향 하중은 없다. 그림에서 연결부 D의 수직변위 δ는 거리 DD' 이다. 점선 AD'와 CD'는 변형 후 트러스 배치이다. 연결부 D의 변위선도(displacement diagram)가 그림 2b에 도시되어 있다. 선 DD₁과 DD₂는 각각 봉 CD와 AD의 늘음(elongation)을 나타낸다. 이 선도로부터 경사봉의 늘음은
\[DD_1=DD_2=\delta\cos\beta\]
이다. 따라서 경사봉의 반력 F₁은
\[F_1={EA\delta\cos\beta\over L/\cos\beta}={EA\delta\cos^2\beta\over L}\qquad\cdots(2)\]
이고 수직봉의 반력 F₂는
\[F_1={EA\delta\over L}\qquad\cdots(3)\]
이다. 식 (2)와 (3)은 하나의 미지수, 즉 변위 δ의 항으로 봉 하중을 표현하고 있다.
이 해법의 다음 단계는 평형 방정식을 얻는 것이다. 연결부 D의 자유물체도(그림2c)로부터 다음을 알 수 있다.
\[2F_1\cos\beta+F_2=P\]
윗식에 F₁과 F₂의 표현식(식 (2)와 (3))을 대입하면 다음 식을 얻는다.
\[{2EA\delta\cos^3\beta\over L}+{EA\delta\over L}=P\]
\[\delta={PL\over EA(1+2\cos^3\beta)}\]
이 해법의 마지막 단계로 δ에 대한 윗 식을 식 (2)와 (3)에 대입하여 봉 하중 F₁과 F₂를 결정한다.
 |
| 그림 3 강화 콘크리트 받침대 예제 (강성법 해석) |
<풀이> 이 구조를 강성법으로 풀기 위해 강체판을 제거하고 그것의 작용을 강과 콘크리트에 의해 전달되는 각각의 하중인 두 힘 Ps와 Pc로 대체한다(그림 3c). 이 하중들을 정적 평형만으로 구할 수 없기 때문에 이 받침대는 정적 부정정이다(그림 3d의 자유물체도 참조). 따라서 받침대 상단의 수직처짐 δ를 미지의 변위로 선정한다. 이 처짐은 받침대의 단축과 같으므로 힘 Ps와 Pc는 δ의 항으로 다음과 같이 쓸 수 있다:
\[P_s={E_sA_s\delta\over h}\qquad P_c={E_cA_c\delta\over h}\qquad\cdots(3)\]
여기서 As와 Ac는 각각 강과 콘크리트의 단면적을 나타낸다. 평형방정식(그림 3d로부터)에 식 (3)을 대입하면
\[P_s+P_c={E_sA_s\delta\over h}+{E_cA_c\delta\over h}=P\]
이 식으로부터
\[\delta={Ph\over E_sA_s+E_cA_c}\]
이다. 윗 식을 식 (3)에 대입하면 수직힘들에 대한 다음 식을 얻는다.
\[P_s={E_sA_s\over E_sA_s+E_cA_c}P\qquad P_c={E_cA_c\over E_sA_s+E_cA_c}P\]
이렇게 힘들과 변위가 구해 졌으므로 강성법에 의한 풀이는 완료되었다.
하지만 이 예제에 있어서 강곽 콘크리트의 응력 σs와 σc를 구하는 것 또한 필요하다(허용하중을 구하기 위해서).
\[\sigma_s={P_s\over A_s}={E_sP\over E_sA_s+E_cA_c}\qquad\sigma_c={P_c\over A_c}={E_cP\over E_sA_s+E_cA_c}\]
각 방정식은 하중 P에 대해서 각 재료의 응력항으로 풀 수 있다.
\[P=\left(A_s+{E_c\over E_s}A_c\right)\sigma_s\qquad P=\left(A_c+{E_s\over E_c}A_s\right)\sigma_c\qquad\cdots(4)(5)\]
이 식들로부터 강과 콘크리트의 허용응력을 기준으로 하중 P의 허용치를 구할 수 있다. 이 두 하중 중에 작은 것이 받침대의 허용하중 P가 된다. 따라서 이 하중 P의 계산은 다음과 같다. 강(12개의 봉)과 콘크리트의 면적들은
\[\begin{split}A_s&=12\left({\pi d^2\over4}\right)=3\pi(25\rm\ mm)^2=5,890\ mm^2\\A_c&=b^2-A_s=(0.5\rm\ m)^2(1,000)^2-5,890=244,100\ mm^2\end{split}\]
이다. 또한 탄성계수 비는
\[{E_s\over E_c}=8\]
허용응력뿐만 아니라 이 값들을 식 (4)(5)에 대입하면 하중 P의 두 값이 산출된다.
\[\begin{split}P&=\left(A_s+{E_c\over E_s}A_c\right)\sigma_s=\left(5,890\rm\ mm^2+{244,100\over8}\ mm^2\right)70\rm\ MPa=2.55\ MN\\P&=\left(A_c+{E_s\over E_c}A_s\right)\sigma_c=(244,100\rm\ mm^2+8\times5,890\ mm^2)8\ MPa=2.33\ MN\end{split}\]
첫번째 결과는 강의 허용응력 기준이고 두번째는 콘크리트의 허용응력 기준이다. 허용하중 P는 이 두값 중에 작은 것이다:
\[P_{\rm allow}=2.33\ {\rm MN}\]
이 하중에서 콘크리트의 응력은 8 MPa(허용응력)이고 강의 응력은 그의 허용응력 아래이다. 왜냐하면 콘크리트 내에서 강에 작용하는 응력은 (2.33/2.55)(70 MPa)=64 MPa 이기 때문이다.



댓글
댓글 쓰기