전단응력과 변형률 (Shear Stress and Strain)
전단응력이 존재하는 실용적인 예를 들어 그림 1a와 같은 볼트 연결을 생각한다. 이 연결은 평판 A, U형 고리 C 및 평판과 고리를 관통하는 볼트 B로 구성된다. 인장하중 P의 작용으로 평판과 고리는 지지된 상태로 볼트를 누르게 되고, 측압응력(bearing stress)이라 부르는 접촉응력(contact stress)이 볼트에 대해 발생한다. 볼트의 자유물체도(그림 1b)는 이 측압응력을 보여준다. 볼트에 대한 측압응력의 실제 분포는 결정하기 어려우므로 응력이 균일하게 분포하는 것으로 단순화 하였다. 균일분포의 가정하에 전체 힘을 측압면적으로 나누어 평균 측압응력을 계산할 수 있다. 이 면적은 측압 곡면을 투영한 것으로 이 경우는 사각형이 된다.
 |
| 그림 1. 직접 전단을 받는 볼트 |
그림 1b의 자유물체도는 단면 mn과 pq를 따라 볼트를 전단하려는 경향이 있음을 보여준다. 자유물체도의 mnpq 부위(그림 1c)로부터 전단력(shear force) V는 볼트의 절단면에 걸쳐 작용해야 함을 알 수 있다. 본 예에서 각 전단력 V는 P/2와 같다. 이 전단력들은 사실 볼트의 단면에 걸쳐 분포된 전단응력의 합력(resultants)들이다. 단면 mn 상의 전단응력들이 그림 1d에 작은 화살표들로 보여지고 있다. 이 응력들의 정확한 분포는 알 수 없지만 중앙부근이 가장 높으며 외각 어딘가에서 영이 될 것이다. 전단응력은 통상 그리스 문자 τ(tau)로 표시한다.
볼트 단면의 평균 전단응력은 전체 전단력 V를 그것이 작용하는 면적 A로 나누어 구한다.
\[\tau={V\over A}\]
그림 1의 예에서 전단력은 P/2 이고 면적 A는 볼트의 단면적이 된다. 이 식으로부터 전단응력은 수직응력처럼 힘의 강도 또는 단위면적 당 힘을 나타낸다. 따라서 전단응력의 단위는 수직응력과 같이 USCS 단위계로 psi 또는 ksi, SI 단위계로 파스칼(pascal) 이다.
그림 1a와 같은 하중조건은 직접전단(direct shear) 또는 단순전단(simple shear)의 예이고, 여기서는 재료를 절단하려는 직접적인 힘의 작용에 의해서 전단응력이 생기게 된다. 직접전단은 볼트, 핀, 리벳, 키, 용접 및 접착연결의 설계에서 발생한다. 전단응력은 또한 부재가 인장(tension), 비틀림(torsion) 및 굽힘(bending)을 받을 때 간접적으로도 발생한다.
 |
| 그림 2. 전단응력과 변형률 |
전단응력 작용에 대해 좀 더 완전한 그림을 얻기 위해서 재료의 변 갈이가 Δx, Δy 및 Δz인 사각 평행6면체 미소요소를 생각한다(그림 2a). 이 요소의 전후면은 어떠한 응력도 없다고 가정한다. 이제 전단응력 τ가 요소 상면에 균일하게 분포되었다고 하자. 그러면 요소의 x방향 평형을 위해서 동일하지만 반대방향인 전단응력이 하면에 작용하여야 한다. 상면의 전체 전단력은 τΔxΔz 이고 이 힘은 하면의 동일하고 방향이 반대인 힘과 균형을 이룬다는 것에 주목한다. 이 두 힘들은 z축에 관하여 크기 τΔxΔyΔz의 모멘트를 갖는 그림의 시계방향 우력(couple)을 형성한다. 요소의 평형은 이 모멘트가 요소의 측면에 작용하는 전단응력의 결과로 동일한 반대 모멘트와 균형을 이룰 것을 요구한다. 측면의 응력을 τ'로 표기하면 수직전단력들은 τ'ΔyΔz 이고 τ'ΔxΔyΔz 모멘트의 시계 반대방향 우력을 형성한다. 모멘트 평형으로부터 τ'=τ 이므로 요소 네면의 전단응력들의 크기는 그림 2a에서 보는 바와 같이 동일하다. 따라서 다음과 같은 결론에 도달한다:
2. 요소 수직 면의 전단응력들은 동일한 크기이고 면들의 교선을 향하거나 멀어지는 방향을 갖는다.
이 전단응력에 관한 결론들은 요소면에 수직응력이 작용할 때도 또한 유효하다.
그림 2a와 같이 전단응력만을 받는 요소를 순수전단(pure shear) 상태에 있다고 말한다. 이 전단응력의 작용 하에 재료는 변형하여 전단변형(shear strains)을 나타낸다. 이 변형률을 가시화하기 위해서 먼저 전단응력은 x, y 및 z 방향으로 요소를 늘리거나 수축시키지 않는다는 것에 유의한다; 다시 말하면 요소 변들의 길이는 변하지 않는다. 대신 전단응력은 그림 2b와 같이 요소의 형상을 변화시킨다. 원래 요소는 경사 평행6면체로 변형되고, 전면은 장사방형(rhomboid)이 된다. 변형전 면 사이 각도 π/2는 미소각도 γ 만큼 줄거나 늘어 π/2-γ가 되거나 π/2+γ가 된다. 이 각도 γ가 요소 형상의 변화나 뒤틀림의 측정치가 되고 전단변형률(shear strain)이라 부른다. 전단변형률의 단위는 라디안(radian)이다.
그림 2에 보이는 전단응력과 변형률의 방향은 양(positive)으로 간주한다. 이 부호규약(sign convention)을 분명히 하기 위해서 축의 양의 방향으로 향하는 면을 요소의 양의 면으로 참조한다. 다시 말하면 양의 면은 좌표축의 양의 방향으로 향하는 바깥 방향 법선(outward normal)을 가지고 있다. 그 반대면은 음의 면이 된다. 따라서 그림 2a에서 우측면, 윗면 및 정면은 각각 양의 x, y 및 z면 이고, 그 반대면들은 음의 x, y 및 z면 이다. 이 용어법을 사용하여 다음과 같이 전단응력 부호규약(sign convention for shear stress)를 서술할 수 있다: 요소의 양의 면에 작용하는 전단응력은 그의 방향이 양의 좌표축으로 향하면 양이고 음의 좌표축으로 향하면 음이다. 요소의 음의 면에 작용하는 전단응력은 그의 방향이 음의 좌표축으로 향하면 양이고 양의 좌표축으로 향하면 음이다. 따라서 그림 2a에 나타난 모든 전단응력은 양이다.
전단변형률 부호규약(sign convention for shear strain)은 응력의 그것과 관계가 있다. 요소의 전단변형률은 두 양의 면(또는 음의 면) 사이 각이 감소할 때 양이다. 요소의 전단변형률은 두 양의 면(또는 음의 면) 사이 각이 증가할 때 음이다. 따라서 그림 2b에 나타난 전단변형률은 양이고, 양의 전단응력은 양의 전단변형률을 만든다는 것을 알 수 있다.
재료의 전단물성은 직접 전단시험이나 비틀림 시험으로 실험적으로 결정될 수 있다. 후자의 시험은 중공원형관(hollow, circular tube)을 비틈으로써 순수 전단응력 상태를 유도한다. 이들 시험의 결과로 전단응력-변형률 선도(stress-strain diagram in shear)를 얻을 수 있다. 이 τ vs γ 선도는 동일 재료 인장시험의 σ vs ε와 유사한 형태를 갖는다. 이 전단선도로부터 비례한도, 항복응력 및 극한응력 같은 전단물성을 얻는다. 이 물성들은 통상 인장의 그것들의 반 정도 값을 갖는다. 예를 들면 구조강의 전단 항복응력은 인장 항복응력의 0.5에서 0.6 배이다.
전단응력-변형률 선도의 초기 구간은 인장에서와 같이 직선이다. 이 선형탄성 범위에서 전단응력과 전단변형률은 직접 비례하고, 전단에서의 후크의 법칙(Hooke's law in shear)으로 다음식을 얻는다.
\[\tau=G\gamma\]
여기서 G는 전단탄성계수(shear modulus of elasticity)(혹은 강성계수(modulus of rigidity)로 불리운다). 전단탄성계수 G는 인장계수와 같은 단위를 갖는다. 즉, USCS 단위계로 psi 또는 ksi이고 SI 단위계로는 pascal 이다. 연강의 통상적인 G값은 11,000 ksi 또는 75 GPa; 알루미늄의 통상적인 값은 4,000 ksi 또는 28 GPa 이다.
인장과 전단탄성계수(E와 G)는 다음식과 같은 관계를 갖는다.
\[G={E\over2(1+\nu)}\]
여기서 ν는 포아송 비(Poisson's ratio)이다. 후크의 법칙에서 유도된 이 관계식은 E, G와 ν가 독립적이지 않은 재료의 탄성 특성이라는 것을 보여 준다. 일반적으로 재료의 포아송 비 값은 영에서 1/2 사이 이므로 위의 식으로부터 G는 E의 1/3부터 1/2가 되어야 한다.
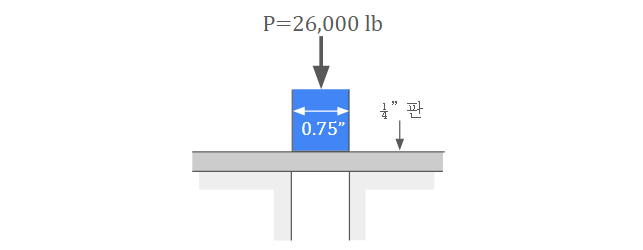
[예제 1] 직경 0.75 in. 펀치가 1/4 in. 강판에 구멍을 가공하는데 사용된다. P=26,000 lb의 힘이 요구된다. 판의 평균 전단응력과 펀치의 평균 압축응력은 얼마인가?
 |
| 그림 3. 예제 1 |
<풀이> 평균 전단응력은 힘 P를 펀치에 의해 전단되는 면적을 나누어 구할 수 있다. 이 면적은 구멍의 원주에 판의 두께를 곱한 것과 같으므로 평균 전단응력은
\[\tau={P\over A_s}={26,000\over\pi(0.75)(0.25)}=44,100\ \rm{psi}\]
이다. 또한 펀치의 평균 압축응력은
\[\sigma={P\over A_c}={26,000\over\pi(0.75)^2/4}=58,852\ \rm{psi}\]
여기서 Ac는 펀치의 단면적이다.
[예제 2] 두께 h이 유연한 재질로 구성된 베어링 패드가 수평 전단력 V를 받는 a×b 치수이 얇은 강판으로 덮어져 있다(그림 4). 패드의 평균 전단응력과 변형률, 그리고 판의 변위 d를 결정하여라.
 |
| 그림 4. 예제 2 |
평균 전단응력은 힘 V를 그것이 작용하는 면적으로 나눈 것과 같다.
\[\tau={V\over ab}\]
해당 전단변형률(패드를 가로질려 균일하다고 가정된)은
\[\gamma={\tau\over G}={V\over abG}\]
이다. 여기서 G는 재료의 전단계수이다. 최종적으로 변위 d는 h tanγ와 같다. 하지만 γ가 미소 각도이면 tanγ를 γ 자신으로 대신할 수 있고
\[d=h\gamma={hV\over abG}\]
를 판의 수평변위로 얻는다.



댓글
댓글 쓰기